Area sokszögek - dolgozat, 9. oldal
1.6 equidecomposability háromszög. Tétel Bolyaya-Gervin
Sok tételek és formulák geometria alapján igazolni vágó formák, majd változó részeik - emlékszik például Pitagorasz-tétel. Ha a két szám vágható ugyanazokat a részek (azaz. E. részei között ezeket meg is lehet állítani az egyben megfelelés, amelyben a megfelelő részek egyforma), ezek a számok nevezzük equidecomposable. Equidecomposable számok, természetesen, egyenlő területű - ezek ugyanazon a területen. Sokszögekhez, az ellenkezője igaz a tétel: bármely két sokszög egyenlő equi. 1832-ben ő bizonyult a magyar matematikus Bolyai Farkas, és egy évvel később, de attól függetlenül is, a német GP Gervin. A legfontosabb, hogy a bizonyíték - újrarajzoláskor téglalap ábra 1.40: vágás „alacsony” téglalapot két háromszögre és egy ötszög, háromszögek mentén elcsússzon ferde szakasz vonal, megkapjuk a másik, a „nagy” téglalapot.
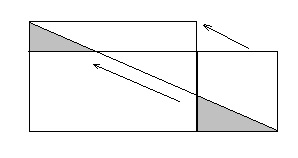
Ily módon, a téglalap nem nehéz átalakítani szinte bármilyen más egyenlő, hogy - ha csak azt, hogy egy új dobozt a „fent” az eredeti, de nem több, mint kétszerese. Ha az arány a magasságok téglalapok kettőnél nagyobb (ábra. 1,41, a) „alacsony”, hogy „hogy a magasabb” egy egyszerű transzformációs (ábra. 1,41, b) ismételten alkalmazzák.
Most már bármilyen sokszög tudjuk dolgozza át a téglalapot valamilyen fix magasságú h. vágjuk háromszögek, minden háromszög átalakulni egy téglalapot (ábra. 1,42), bemutatjuk téglalapok kapott állandó H magassággal és sostykuem függőleges oldalai.
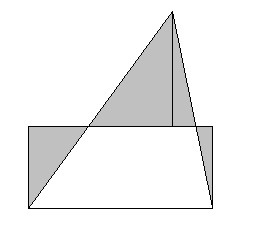
Ha két háromszög egyenlő területű, a dobozok megfelelő állandó h magasságú egyenlő. Így ezek a sokszögek equi azonos alak, és onnan, akkor megállapíthatjuk, hogy azok equi együtt.
1.7 A területének aránya a hasonló háromszögek
1. Tétel A terület a két háromszög az egyenlő sarokban, mint munkái felek kössenek ezek sarkait.
Bizonyítás. Legyen az ABC háromszög, és a (ábra. 1,43), az A és B szögek egyenlő.
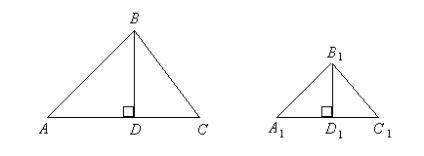
Fürdőzés után a magasságot, és mi van:
Háromszögek és hasonló ( A és A1 = D = D1 = = 0-tól 90), azonban; cseréje a második első kapcsolat, ezt kapjuk:
2. Tétel A területeket a hasonló sokszögek, mint négyzetek egybevágó oldalán.
Bizonyítás. 1) Ha - két hasonló háromszögek, a szögek a sarkok, illetve a másik; hagyja, hogy a
Rájuk az előző tétel:
De mivel a hasonlóság háromszögek alábbiak szerint:
Ezért az egyenlet (1.14) tudjuk az egyes kapcsolatok és a helyére tetszőleges számú kapcsolatban (1,15), ezért
2) Ha az (a ábra 1,44.) - két hasonló sokszög, akkor meg lehet oldani az azonos számú egymástól egyenlő távolságban lévő és a hasonló háromszögek.
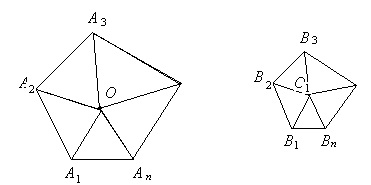
Legyenek ezek háromszög:
Az alapján, amit már bizonyított az első része ennek a tételnek, megkapjuk arány:
De mivel a hasonlóság a poligonok kell:
Következmény. Szögletes helyes poligonok ugyanaz a neve, mint az oldalán a tér, vagy négyzetek apofem sugarak.
1.8Figury a legnagyobb területet
1.8.1 vonal vagy téglalap
Ezt figyelembe véve tétel kezdeni a probléma megoldásának.
Feladat. A végzetes nap az életében Lágyéki eltelt 40 versztányira, séta oldalán a trapéz területe 78 négyzetméter versztányira. Eredeti szándéka az volt, hogy az oldalán egy téglalap, trapéz van kapcsolva véletlen, hiszen a kedvezőtlen számítás. Érdekes, hogy meghatározza: erősítés ő vagy elszámította magát, hogy a helyszínen nem volt egy téglalap, trapéz? Ebben az esetben meg kell kaptak egy nagy területen a föld?
Határozat. A kiiktatott dobozok 40 szellőzőnyílás lehet sok, és minden más a környéken.
Íme néhány példa:
14 6 = 84 sq. szellőzők
13 7 = 91 sq. szellőzők
12 8 = 96 sq. szellőzők
11 9 = 99 sq. szellőzők
Látjuk, hogy az összes ezeket a számokat az azonos kerülete 40 versztányira területe nagyobb, mint a mi trapéz. Azonban, az ilyen téglalapok lehetséges kerülete 40 szellőzők, amelynek területe kisebb, mint a trapéz:
18 2 = 36 nm. szellőzők
19 1 = 19 sq. szellőzők
19,5 0,5 = 9,75 téren. szellőzők.
Következésképpen az a kérdés, a probléma az, lehetetlen, hogy határozott választ. Vannak dobozok egy nagyobb területet, mint a trapéz, de vannak kevésbé ugyanabban az perifériáján. De lehet, hogy egy nagyon határozott választ arra a kérdésre: melyik a téglalap alakú egy adott kerületre magában foglalja a legnagyobb területet? Összehasonlítva a doboz, azt látjuk, hogy minél kisebb a különbség a oldalhosszához, a terület egy téglalap hosszabb. Ez természetes, hogy következtetni, hogy ha ez a különbség egyáltalán nem így van. E. Ha a téglalap lesz egy négyzet területe a szám eléri a maximális értéket. Ezt követően egyenlő 10 10 = 100 sq. szellőzők. Könnyen belátható, hogy ez a tér valóban kiváló a terület minden téglalap egyenlő a kerülete is. Pahomu kell menni az oldalán a tér, hogy a legnagyobb földterület - 22 négyzet mérföld több, mint tudott elérni.
1.8.2Zamechatelnoe tér ingatlan
A figyelemre méltó tulajdonsága a tér - zárt határai a legnagyobb területen, mint az összes többi rovatban az azonos területet. Adunk egy alapos bizonyíték.
Jelöljük a kerülete egy téglalap alakú keresztül R. Ha veszel egy négyzet kerületét, mindkét oldalán kell lennie. Azt bizonyítja, hogy lerövidíti az egyik oldalon, hogy néhány érték b ugyanabban meghosszabbítása a szomszédos oldalán, megkapjuk egy téglalapot az azonos kerületi vele, de egy kisebb területen. Más szóval, azt bizonyítják, hogy a terület egy négyzet nagyobb, mint a terület egy négyszög:
Mivel a jobb oldalon ez az egyenlőtlenség, akkor az egész kifejezés válik: vagy.
De az utolsó egyenlőtlenség nyilvánvaló: a tér minden mennyiségben, pozitív vagy negatív, nagyobb, mint nulla. Következésképpen az igazi és eredeti egyenlőség, ami vezetett bennünket, hogy ezt.
Így a tér a legnagyobb területe a téglalap azonos területet.
Ebből következik, hogy az összes négyszögletes formák az ugyanazon a területen a tér a legkisebb kerülete. Ez látható az alábbi érvelés. Tegyük fel, hogy ez nem igaz, és hogy van egy téglalap egyenlő A. amely téren terület kerülete kisebb, mint azt. Ezután, a rajz a négyzet ugyanaz kerülete, amely a téglalap A. kapjunk egy négyzet, amelynek egy nagyobb területen, mint A., és ezért nagyobb, mint egy négyzet V. Ennek eredményeként azt találták, hogy egy négyzet C van egy kerülete kisebb, mint a négyzet B. és a terület nagyobb, mint ő. Ez nyilvánvalóan lehetetlen: idő tér oldalán kisebb, mint az oldalán a tér és az V. területet kisebbnek kell lennie. Így lehetetlen volt bevallani, hogy léteznek a téglalap A, amely ugyanazon a területen van egy kerülete kisebb, mint a tér. Más szóval, az összes téglalapokat ugyanazon a területen a legkisebb a kerülete a négyzeten.
Ezek ismerete tulajdonságokkal négyzet segített Pahomu pontosan kiszámítani az erők, és kap egy téglalap alakú terület legnagyobb területen. Tudva, hogy tudja átadni egy nap anélkül, stressz, például a 36 szellőzőnyílás, ő megy a határ mentén egy négyzet oldala 9 mérföldre, és este lenne a tulajdonos a helyszínen a 81 négyzet mérföld - 3 négyzet mérföld több, mint ő kapott halálos megterhelés. Ezzel szemben, ha ez volt, csak előre, hogy adott területen a téglalap alakú terület, például 36 nm versztányira, lehetett elérni eredményt a legkisebb energiafelhasználással, megy át a határt egy négyzet, amelynek oldalai - 6 nyílásokat.