eltérés jellemzői
Hadd differenciálható az x. Definíció szerint a származék. Szerint a kapcsolatot határeloszlástételt infinitezimális. ahol mikor. Megszorozzuk mindkét fél által # 8710; x:
(1), ahol # 8710; x → 0. .
Hasonlítsa össze ezeket a parányi:
Ha. majd # 8710; x - BM ugyanabban a sorrendben
2) - BM magasabb rendű # 8710; x.
Így a növekmény a függvény # 8710; y értéke 2 x szempontjából: az első a fő része a növekmény funkciót. lineáris tekintetében # 8710; x; és a második tag - végtelenül magasabb rendű # 8710; x.
Definíció. Differenciál a függvény a ponton x a-származék a termék ezen a ponton az érv növekmény # 8710; x.
Találunk a differenciál a funkciót. mert . akkor. azaz. (3)
Differenciál dx független változó x egybeesik inkrementálisan # 8710; x.
Formula (2) a (3) válik: (4) - a differenciál funkciót.
Így - (Leibniz jelölés).
Függvény deriváltját lehet tekinteni, mint az arány a differenciál függvény a differenciális a független változó.
13. §. A geometriai jelentése a differenciál.
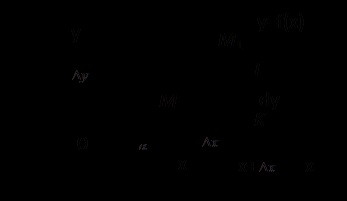
Ahhoz, hogy egy grafikon, egy pont M (x, y) készít egy érintő.
# 945; - dőlésszöge érintő a Ox tengellyel.
Adjunk x növekmény # 8710; x. akkor a függvény növekszik # 8710; y. A görbe megkapjuk egy pontot az M1 (x + # 8710; x, y + # 8710; y), KT - ordináta növekmény tangensét.
|
. Differenciál funkciók a növekmény m x ordináta a átmenet az érintési pont a abszcissza x a ponton az abszcissza x + # 8710; x.
Differenciális formában invariancia (függetlenség eltérés felvétel formák).
1) Legyen. X - független változó
2) Legyen. x = x (t) - függvényében t.
- bonyolult függvénye, X - egy köztes álláspontot.
(A szabály szerint a differenciáló kompozit funkció)
A képletekben (1) és (2) rögzítése a differenciális alakja azonos. eltérés tulajdonsága, melynek formája ugyanaz az írás függetlenül attól, hogy x a független változó, vagy a funkció egy másik változó nevezzük egy invariáns differenciális formában.