Feladatok körülbelül területe a téren, és több
Ez meglepő és ismerős téren. Ez szimmetrikus geometriai tengelye körül, és végrehajtani átlósan közepén keresztül és oldalát. A keresési terület négyzet vagy térfogata általában nem túl nehéz. Különösen, ha ez ismert oldalhosszúságú.
Néhány szó a szám és tulajdonságai
Az első két tulajdonságok társított definíció. Minden oldalról a szám egyenlő egymással. Végtére is, a tér - ez a megfelelő téglalapot. És ő, hogy minden fél egyenlő, és a szögek egyenlő fontosságú, nevezetesen - 90 fok. Ez a második tulajdonság.
A harmadik kapcsolódik a hossza a átlók. Ők is egyenlő egymással. És metszik derékszögben közepén a pontokat.
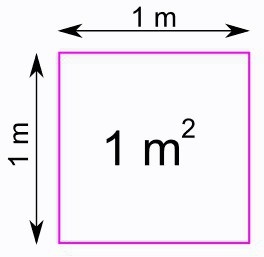
A formula, amely csak az oldalsó hossza
Először is, a kijelölés. A hossza az oldalán hozott választani a levél „a.” Ezután, egy négyzet alakú területet alábbi képlettel számítottuk ki: S = a 2.
Könnyen nyert az egyik, hogy ismert a téglalap. Ebben a hosszát és szélességét meg kell szorozni. A tér, ez a két elem egyenlő. Ezért, ebben a képletben jelenik meg egy-négyzet-értéke.
Formula, ahol az átlós hossza szerepelt
Ez az átfogó egy háromszög, amelynek oldalai a lábak az ábra. Ezért tudjuk használni a Pitagorasz-tétel egyenlet és kimeneti, ahol az oldalsó által kifejezett egy átlós.
Miután egy ilyen egyszerű átalakítások, azt találjuk, hogy a terület egy négyzet keresztül átlós értékét a következő képlet szerint:
S = d 2/2 Itt, a levél d jelöli a négyzet átlójának.
a kerületük mentén a képlet
Egy ilyen helyzetben szükség van, hogy kifejezze az oldalán keresztül a kerületi és helyettesíteni azt a területet képlet. Mivel ugyanazon az oldalon az ábrán négy, a kerület lesz, hogy elosztjuk 4. Ez az érték kerül a kéz, amelyet azután behelyettesíthetjük a kezdeti, és számolja a területet a tér.
A képlet általánosságban a következő: S = (P / 4) 2.
Kihívások a számítások
1. szám van egy négyzet. A összege annak két oldala egyenlő 12 cm. Számítsuk ki a terület a tér és a kerülete.
Határozat. Mivel adott az összeget a két fél között, azt kell tudni, hogy a hossza egy. Mivel azok azonosak, bizonyos számú, csak meg kell osztani két. Azaz az oldalán a szám 6 cm.
Ezután a kerület és a terület könnyen kiszámítható a következő képlet segítségével. Az első a 24 cm-es, és a második - 36 cm 2.
Válasz. A kerülete a tér 24 cm, és környékén - 36 cm 2.
2. számú megtudja területe egy négyzet kerülete 32 mm.
Határozat. Egyszerűen helyettesítse a kerület értékét a képlet fent leírt. Bár meg lehet tanulni az első oldalán a tér, és csak ezután a területet.
Mindkét esetben az intézkedések fog menni az első osztály, majd hatványozás. Egyszerű számítások vezet az a tény, hogy a terület képviseli tér 64 mm2.
Válasz. A keresési terület 64 mm2.
3. számú négyzet 4 dm. A négyszög méretek: 2 és 6 dm. Ezek közül melyik két számadat nagyobb területet? Hányan voltak?
Határozat. Hagyja, hogy a oldalán a tér jelzi a levél A1. akkor a hossza és szélessége a téglalap A2 és B2. Ahhoz, hogy határozza meg a területet egy négyzet érték a1 állítólag négyzet és a téglalap - többszörösen A2 és B2. Ez egyszerű.
Kiderült, hogy a terület a tér 16 dm 2, és a téglalap - 12 dm 2 Nyilvánvaló, hogy az első szám nagyobb, mint a második. Ez annak ellenére így van, hogy azok egyenlő területű, vagyis azonos területet. Hogy ellenőrizze, akkor lehet számolni a kerület. A tér oldalán meg kell szorozni 4, kapsz egy 16 dm. A téglalap hajtogatott oldal és szorozzuk meg 2 lesz ugyanazt a számot.
A probléma az, hogy válaszoljon még, hogy milyen sok területen eltérő. Ahhoz, hogy ezt a számot levonjuk a nagyobb kevesebb. A különbség egyenlő 4 dm 2.
Válasz. Területe 16 dm 2 és 12 dm 2 A tér több, mint 4 dm 2.
A kihívás a bizonyítási
Állapotban. A katéterek egyenlő szárú derékszögű háromszög épített tér. A beépített átfogója magasság, ahol egy másik téren épült. Bizonyítsuk be, hogy az első terület kétszer nagyobb, mint az utóbbi.
Határozat. Bemutatjuk a jelölést. Hagyja, hogy a láb egy, magassága felhívjuk az átfogó, x. A terület a tér - S1. a második - S2.
A terület a tér épül a katéterek számítják egyszerűen. Ez egyenlő értékű 2. Egy második, nem olyan egyszerű.
Először meg kell tudni, hogy a hossza átfogója. Erre praktikus képletet a Pitagorasz-tétel. Egyszerű transzformációk vezet a következő kifejezés: a√2.
Mivel a magassága egyenlő oldalú háromszögben hívni a bázis, az is a medián és a magasság, hogy megosztja a nagy háromszög két egyenlő szárú derékszögű háromszög. Ezért a magasság felével egyenlő az átfogó. Azaz, X = (a√2) / 2. Ezért könnyű tudni a területet S2. Azt találtuk, hogy a 2/2.
Nyilvánvaló, hogy a mért értékek eltérnek pontosan kétszer. És a második alkalommal ez a szám kevesebb. QED.
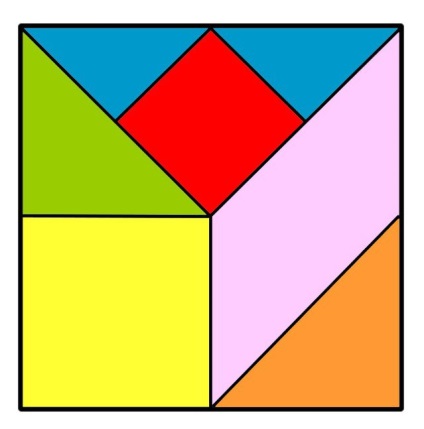
Egy szokatlan kirakós játék - Tangram
Ez történt a téren. Meg kell konkrét szabályok alapján vágva különböző alakzatokat. Az összes alkatrész legyen 7.
Azt jelenti, hogy a játék fog használni minden megkapta a terméket. Közülük kell más geometriai formák. Például, téglalap, trapéz vagy paralelogramma.
De még ennél is érdekesebb, ha a darabok olyan állatokból származnak, vagy tárgyak körvonalait. És kiderül, hogy a terület a számadatok származik az egyik, hogy a kezdeti téren.
