Tétel a háromszög területén a bizonyítékok és a problémamegoldás
A háromszög területe egyenlő fele a terméket az oldalán a sine a szög között.
Tekintsünk egy tetszőleges ABC háromszög. Let it másikra BC = a, oldalsó és CA = b S - terület a háromszög. Meg kell azt mutatják, hogy az S = (1/2) * a * b * sin (C).
Kezdeni, akkor be egy derékszögű koordináta-rendszert, és helyezze a származás, a C pontban rendezzük a koordináta-rendszert úgy, hogy a B pont feküdt a pozitív irányba Cx tengely, és az A pont lenne pozitív ordináta.
Ha helyesen tette, akkor kap a következő kép.
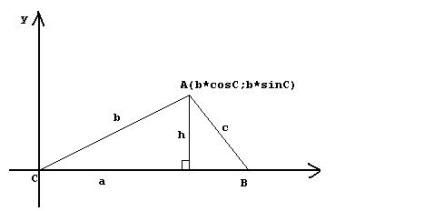
A terület a háromszög lehet kiszámítani a következő képlet segítségével: S = (1/2) * a * h. ahol h - a magassága a háromszög. Ebben az esetben, a h magasság a háromszög egyenlő az ordináta a pont, azaz h = b * sin (C).
Figyelembe véve a kapott eredmény, a háromszög terület formula átírható a következőképpen: S = (1/2) * a * b * sin (C). QED.
Megfelelni a kihívásoknak
Probléma 1. Find a ABC háromszög területe, ha a) AB = 6 * √8 cm, AC = 4 cm, a szög = 60 ° b) BC = 3 cm, AB = 18 * √2 cm, a B szög = 45 ° ) AC = 14 cm, CB = 7 cm, C = szöge 48 fok.
A fenti tétel háromszög területén S ABC:
a) S = ((1/2) * 6 * √8 * 4 * sin (60˚)) = 12 * √6 cm ^ 2.
b) S = (1/2) * BC * BA * sin (B) = ((1/2) * 3 * 18 * √2 * (√2 / 2)) = 27 cm ^ 2.
a) S = (1/2) * CA * CB * sin (C) = ½ * 14 * 7 * sin48˚ cm ^ 2.
A sine a szög nézet, hogy a számológép vagy használja az értékeket a táblázat trigonometrikus szögek. válaszolni:
c) körülbelül 36,41 cm ^ 2.
Probléma 2. Az ABC háromszög területe egyenlő 60 cm ^ 2. Keresse az AB oldalt, ha AC = 15 cm, a szög = 30˚.
Legyen S - ABC háromszög területe. A tétel a háromszög területe, van:
Mi helyettesíti azt kapható értékeink:
60 = (1/2) * AB * 15 * sin30˚ = (1/2) * 15 * (1/2) * AB = (15/4) * AB.
Ezért azt hosszában húzódó oldalsó AB: AB = (60 * 4) / 15 = 16.