Delta funkció - a világ szép
?-funkció - egy általános függvény formálisan definiált folytonos lineáris funkcionális térben differenciálható függvények. funkció nem működik a klasszikus értelemben.
Által bevezetett brit fizikus Dirac. Ez lehetővé teszi a felvétel térbeli sűrűsége a fizikai mennyiség (tömeg, töltés, az intenzitás a hőforrás, és így erőt. P.), vagy koncentrált egy pontban csatlakoztatva. Például, a sűrűsége egy pont m tömegű, egy pont található az euklideszi térben. Meg van írva a help-funkció formájában.
?-funkció által meghatározott kapcsolatban hivatalos
minden folytonos függvény.
A delta függvény egy változó következő egyenletek igazak:
Sok esetben a legkényelmesebb a képviselete a delta függvény:
Tekintsük az integrál
amely úgy értelmezhető, mint egy határ
By (3) bármely egyenlőség:
Belátható, hogy egy korlátlan növekedés helyesek összes tulajdonságait a delta a funkciót, (2) van irányítva, hogy; Ez arra enged következtetni, hogy:
.
Az alapvető kifejeződése, amely leírja egy származéka a delta függvény. (X):
.
Behelyettesítve. Megkapjuk a kifejezést:
.
A transzformáció után van:
.
Mert. A végső expressziós
.
Általában a kifejezés a származékot a delta függvénnyel van írva a következő:
.
A származékot delta függvény már a következő azonosságokat:
;
;
.
Előzetes koordinátái x (t) =. (T) lehet alkalmazni a Fourier-transzformáció:
Az eredmény az, hogy a spektrum-függvény konstans :? (?) F = 1.
Bizonyított, hogy a származék a Heaviside függvény egy delta függvénnyel. Ie látható funkció fenti funkciók:
.
Ezért alkalmazásával Fourier-transzformáció a delta függvénnyel
.
Kapunk az utat a következő formában:
.
A kétdimenziós tér:
;
.
A poláris koordináta:
.
A háromdimenziós térben:
;
.
A hengeres rendszerben:
.
A gömbi koordináta-rendszerben:
.
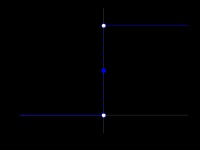
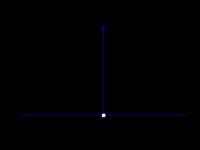
azonnali gyorsulást
Egy példa az alkalmazás a Dirac-delta az a probléma, az ütközés a két testület. Ha a másik swoops hatását, mindkét szerv kap a gyorsulás és a sebesség. Hogyan számoljuk ki a gyorsulás szerzett a szervezetben? Készítünk egy grafikonon az idő mértéke. A grafikon lesz látható formában a felső képen a jobb oldalon. Az alsó ábra egy grafikon, a delta-funkció egység amplitúdó, ez tükrözi a jelen eljárás gyorshívó testet.
Figyelembe véve azt a tényt, hogy a modell tekinthető az euklideszi térben, tudjuk írni a következő egyenletet:
Green függvény
További példák a delta funkciót használjuk a matematikai fizika problémák megoldásában, amelyek magukban foglalják az érték-orientált. A kvázi-klasszikus hullám funkciók lokalizálódnak a delta funkciót, és központjaik a koncentráció mentén mozgó klasszikus pályái newtoni egyenletek. Keresztül a delta függvény, és felvétel funkciók a zöld vonal üzemeltetője L eljáró disztribúciók, mint egy sokrétű M ponton x 0. Az egyenlet az űrlapot.
ahol - Laplace operátor.
Fontos megjegyezni, a következő képlet
.
Ez a kifejezés azt jelenti, hogy úgy viselkedik, mint egy delta függvénnyel. Ez a tény arra használjuk, hogy bizonyítani, hogy a kifejezés skalÆrpotenciÆl:
kielégíti a Poisson-egyenlet:
.
Így a delta függvény egy erőteljes matematikai eszköz leírására bonyolult fizikai folyamatok.