A Newton-Cotes
Ha az integrandust helyettesít interpolációs polinom, megkapjuk a kvadratúra képlet formájában:
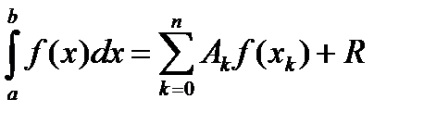
ahol x ^ - kiválasztott interpolációs pontokat; Ak - együtthatók, amelyek függenek a kiválasztott komponensek, de nem függ a típus a f (x); R - fennmaradó, meghatározzuk a maximális hiba segítségével kvadratúra képlet; k = 0, 1, ..., N.
Felosztása az integráció [a, b] n egyenlő részre a pontrendszert
és kiszámítjuk az integrandus a kapott csomópontok
kapnak kvadratúra képletek egyenlő távolságra csomópontok. Ezek a képletek nevezzük Cotes formulák, Newton. A legtöbb kényelmes numerikus integrálása az interpolációs alacsony érdekében polinomot, amelyet úgy kapunk, a viszonylag egyszerű általános képletű vegyületet.
Trapéz kapunk abban az esetben polinom-interpoláció az 1. szabály:
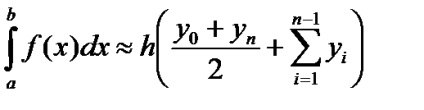
A fennmaradó kifejezés a következő formában: A trapéz szabály a számítás a határozott integrál vezet, amikor tévedésből
Ahhoz, hogy megtalálja egy közelítő értéket a határozott integrál trapéz algoritmus használható, amelynek diagram ábrán szemléltetjük. 5.5.
Hibahatárok a trapéz módszer nagyobb, mint a többi képlet Newton-Cotes, de fellebbezni az egyszerű végrehajtását. Ezen kívül kisebb összetettsége az algoritmus jelentősen csökkenti a hiba kiszámítása azonban trapéz alkalmazott képlet elég gyakran (kombinálva más képletek).
Például, abban az esetben a közelítő integrandust Hermite interpolációs polinom kapott Euler formula:
A fennmaradó ideje ez a képlet azt jelzi, hogy egy kis mellett a trapéz szabály jelentősen növeli a pontosságát.
Ebben a képletben, a származékok helyettesíteni lehet kétoldalú különbségek
Ennek eredményeként a képletű alakítjuk Euler formula Gregory. de az általános rendjét pontosság csökken a negyedik helyről a harmadik.
(2) általános képletű parabola (Simpson)
Használata polinom-interpoláció 2-rendű (parabola) kapjuk numerikus integrálással képletű - Simpson-féle képlet:
Ábra. 5.5 algoritmust a határozott integrál trapéz
Ábra. 5.6 ábra egy diagram, az algoritmus végrehajtási számítási képlet szerint parabola. .. Amikor végrehajtási képletű páratlan csomópontok száma szükséges, azaz a száma, partíció részek integrációs intervallumban kell lennie páros szám: n = 2m. Az algoritmus a recepción, ahol az iterációk számát a felére csökken, azaz a. E. Kétszer a ciklus paraméter módosítás nem valósul meg, ami csökkenti végrehajtási időt az algoritmus. Simpson módszer tekinthető az egyik leggyakrabban használt numerikus integrálási módszerek, amelyek egy viszonylag jó pontossággal számítások.
Ábra. 5.6 algoritmust határozott integrálok képletű Simpson
(3) A Newton (általában 3/8)
Nagyobb pontosság interpolációs számítás előírja integrandusz harmadik fokú polinom. Az eredmény a Newton képletű (tipikusan 3/8):
numerikus integrálással rendszer, amelyben egy algoritmus szerint a jogállamiság 3/8 ábrán látható. 5.7 A gyakorlati alkalmazás találtuk továbbá a negyedik, ötödik és hatodik Formula Newton-Cotes, de a felhasználása oda vezet, hogy egy nehézkes rendszerek.
Ábra. 5.7 algoritmust határozott integrálok Newton-féle képlet