Meghatározása nehézségi gyorsulás segítségével a matematikai inga
Kiadó a távol-keleti Szövetségi Egyetem
E művelet - további jogszabályok és a matematikai inga oszcilláció ismerik a módszert kísérleti meghatározása nehézségi gyorsulás vele.
Rövid elmélet. A mechanikus mozgása szervek - változtatni a helyzetét a térben idővel. Mozgása a test három csoportba sorolhatók:
transzlációs - minden pont a test mozog az azonos (sebesség és a gyorsulás pontokat a test és azonos nagyságú és irányú);
forgatás - az összes pontot a test mozgó körök körül egy közös központ vagy tengelye;
oszcilláló - minden pont a test dugattyús vagy lengő mozgást. M pont nem terjed túl semmilyen otrezkaKLna a vonal, és többször áthalad a ugyanabban a helyzetben ebben az intervallumban (1. ábra) egy lineáris oszcilláló mozgás. Az oszcilláló mozgás jellemzi bizonyos ismétlődő időben. Ha ilyen mozgás létezik egy bizonyos időintervallumban T, amelyen keresztül a mozgás az M pont szerint járunk el, mint a fluktuáció nazyvaetsyaperiodicheskim.
Sok különböző periodikus rezgések a legegyszerűbb, amelyek harmonikus rezgések - rezgések, amelyben a fizikai (vagy bármilyen más) értéke változik szinuszos vagy koszinuszos jog idővel. Harmonikus rezgések - jelentése idealizáció közé tartozott az összes többi rezgés különleges hely, mely annak köszönhető, hogy két oka van:
1) oszcillációk a természetben előforduló és a technológia, gyakran a karakter közel harmonikus rezgések;
2) bármely nem-harmonikus rezgés ábrázolható összegeként (szuperpozíciója) különböző harmonikus rezgések.
A kinematikai egyenlet harmonikus rezgés a formája
Az egyenletek (1) és (2):
X -smeschenie (eltérés) a rezgő pont az egyensúlyi helyzetből, amikor vremenit;
A jelentése a rezgés amplitúdója egy értéket meghatározó a maximális eltérés a rezgő pont az egyensúlyi helyzetből (A = | Hmax |). Amplitúdó és ofszet SI egységekben mérik méter.
gyűrűs frekvencia ω érték számát jelzi a teljes rezgések előforduló techenie2π másodperc. Az SI ciklusos jelentése mért s -1. Ciklikus gyakorisága időszakhoz kapcsolódó és kolebaniyT chastotoyν.
T az az időszak, oszcillációk. értéket meghatározó idő egy teljes oszcillációs (időintervallum két egymást követő járatban egy rezgő pont ugyanabban a pozícióban azonos irányba) = .T. iliω =. Időszakban az SI rendszer másodpercekben mérhető.
ν van az oszcillálás frekvenciáját a számát jelölő érték a teljes rezgések egységnyi idő. A frekvenciája összefüggésben van az időszak és gyakorisága a ciklikus kapcsolatok: ν =. A SI rendszerben, a frekvencia ν mérjük hertz (HERZ egy oszcilláló másodpercenként).
ωt + φo fázisú rezgést érték meghatározására az eltolás értékét rezgő pont az egyensúlyi helyzetből jelenleg vremenit.
φo - kezdeti szakaszban. értéket meghatározó elmozdulás nagyságát a x a rezgő pont az egyensúlyi helyzetből a kezdeti időben (t = 0). A kezdeti fázis és fázis oszcillációk mért szögeltérés egységeket, vagyis a fokban vagy radiánban (a π frakciók).
Használata egyik kinematikai egyenletek harmonikus rezgések, például (1) egyenlet, megkapjuk a kinematikus tulajdonságait ezen ingadozások - sebesség és gyorsulás.
Speed V - az első alkalom származékot az elmozdulás X:
V = = AωCos (ωt + φo), (3)
ahol a nagysága Aω - sebesség-amplitúdója Av harmonikus rezgéseket.
Gyorsítás harmonikus rezgések α úgy definiáljuk, mint az első alkalommal származékot a sebesség harmonikus rezgések, vagy a második származékot az elmozdulás
α = == - Aω2Sin (ωt + φo), (4)
ha ez az érték O2 - gyorsulás amplitúdó Aa. Tekintettel egyenlet (1), a gyorsulás a harmonikus rezgések ((4) egyenlet) lehet kifejezni más formában:
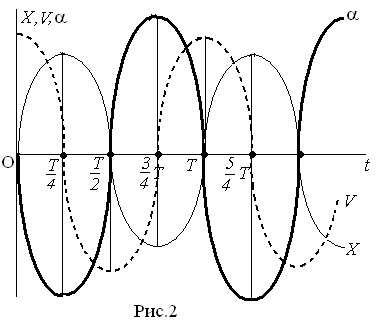
A képletek (1), (2) és (3) azt mutatja, hogy amikor a harmonikus rezgések az elmozdulás, sebesség és gyorsulás jellemzi azonos ciklikus gyakorisága, és így az időszak (T =). Phase ingadozása ezen mennyiségek különbözőek: fordulatszám ingadozás megelőzve a rezgés elmozdulás fázisban (az idő), a rezgés gyorsulás ingadozás előre elmozdulás fázisban π (az idő).
A 2. ábrán grafikonok az elmozdulás ideje, a sebesség és a gyorsulás (kezdeti fázis φo = 0). Amint az ábrából látható, idején áthaladását az oszcilláló helyzetének egyensúlyi pont (X = 0), a maximális sebességet. Ha a maximális pont eltér az egyensúlyi helyzet (X = + A = -A iliH), a sebessége nulla, és a gyorsulás maximális. Ebben az esetben a gyorsulás mindig annak a jele, amely ellentétes az elmozdulás, vagyis gyorsulás mindig irányul az egyensúlyi helyzet a oszcilláló pont.
Ismerve a tömeg mkoleblyuscheysya részecskék (anyagi pont) és annak gyorsítás alábbi egyenlet határozza meg (5), azt találjuk, az erő, amely alatt a harmonikus rezgéseket az elkövetett. Szerint a Newton második törvénye, ez az erő
ahol k = mω2 - arányossági tényező állandó egy adott oszcillátor (oszcillátor - a fizikai rendszer, oszcillálnak). Tól (6) egyenlet azt mutatja, hogy az erő okozza a harmonikus rezgés arányos smescheniyuH és azok ellen irányul a torzítás, amint azt a mínusz jel. Ez az erő igyekszik visszatérni az oszcilláló pont az egyensúlyi helyzetben, így nazyvayutvozvraschayuschey erő. Ilyen erőnek lehet például bytsila rugalmasságát. fordul elő, amikor a kis deformációk bármilyen, amely szerint a Hooke-törvény, arányos a deformáció (elmozdulás) AH és ellenkező előjellel. Visszaállító erők is más, nem rugalmas jellegű. Ezekben az esetekben ezek nazyvayutsyakvaziuprugimi erők (azaz „mintha, mint a rugalmas erők”). Koeffitsientk. értékének meghatározása okozó erő elmozdulás, az úgynevezett együttható visszaállító erőt. Mint egy rugalmas erő, és a kvázi-elasztikus erők belső erők a rezgő rendszer. Sledovatelno.garmonicheskie oszcilláció áll elő az intézkedés alapján belső rugalmas vagy hasonló hozzájuk, quasielastic erők. Ingadozások előforduló csak a hatása alatt belső erők nazyvayutsyasvobodnymi (vagy saját).
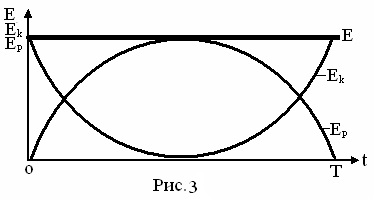
Az energia harmonikus rezgések. A harmonikus rezgések engedelmeskedik a törvény mechanikai energia megmaradás, amely szerint a teljes E energiáját a harmonikus oszcillátor állandó marad. Mi bizonyítja ezt az állítást. Teljes mechanikus energiyaE áll kineticheskoyEk és potentsialnoyEp energia
A mozgási energia olyan intézkedés a mozgás az anyag pont (vagy transzlációs mozgása egy merev test) úgy határozzuk meg, a képlet
ahol m - tömege a rezgő pont, V - a sebesség.
A potenciális energia egy test határozza meg az állam, illetve annak térbeli helyzetét. Az elasztikus (vagy kvázi-elasztikus) kényszeríti a potenciális energia a test határozza meg a képlet
ahol k - a rugalmassági tényező, X - elmozdulása a rezgő pont az egyensúlyi helyzetből.
expresszió a teljes mechanikai energia harmonikus hullámforrást:
A mennyiségek a jobb oldalon az egyenlet (k és A) - állandó a harmonikus oszcillátor, és így a teljes energia a harmonikus oszcillátor kolebaniyE erre állandó. Ugyanakkor, mind a kinetikus és a potenciális energia, változás ellentétes fázisú, megfelelően rendre egy kvadratikus törvény koszinusz és szinusz (ábra. 3).
Inga, az időszak annak oszcillációk. Egy példa a mechanikai rezgések hatása alatt a harmonikus erők quasielastic oszcilláció a matematikai inga. Matematikai inga nevezzük egy idealizált rendszer, amely súlytalan és nyújthatatlan fonál, felfüggesztett tömeget koncentrálódik egy ponton. Egy jó közelítése a matematikai inga egy kis nagy labdát felfüggesztve egy hosszú, vékony, nem-nyújtható fonalak (4. ábra). A labda az inga mindig két erő: gravitációs erő a szálfeszítő. Az egyensúlyi helyzet (szabadon függesztett inga), ezek összege erők egyenlő nullával. Az inga labda, eltért egyensúlyi helyzetben ugolφ. jár visszaállító erő egyenlő a kapott két erők: a gravitációs erő (g-nehézségi gyorsulás), és a fonal feszültsége erők.
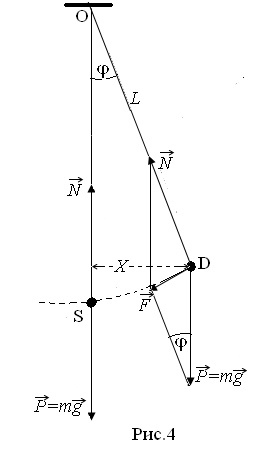
Az intézkedés alapján ezen visszatérítő erő, az inga elkezd gyorsan mozog a pont tochkiD S (egyensúlyi helyzet). Pontban S az az erő nulla, de mivel az inga tömege m, és az idő az áthaladását a pont S van egy sebessége V. tehetetlenség át ezen a ponton. Amikor egy ív további inga mozgási sebessége csökken annak a ténynek köszönhető, hogy az irányt az erő változik az ellenkező irányba az inga mozgását. Végpontban inga mozgás megáll, és azonnal elindul a pont S. Így az inga elvégzi az erő a vibrációs mozgást. Ha az inga nem működik a súrlódási erő, akkor rezegni a végtelenségig. A 4. ábra azt mutatja, hogy silysvyazana értéket a értéke a gravitációs erő, a kapcsolat:
Dependence visszaállító erő elmozdulás ellen, azzal jellemezve, szögben φ, a (11) egyenlet, a nem-lineáris, így a rezgések az inga nem harmonikus. Mindazonáltal a kis rezgések az inga, ha az elhajlás szöge φ olyan kicsi (legfeljebb körülbelül 5), chtoSinφ = ≈ φ. visszaállító erő arányos a szöget φ ebben az esetben (a kis eltérések) feltételezheti, hogy az inga oszcilláció áll elő hatása alatt a kvázi-elasztikus erőt, és így, a rezgés harmonikus. Otkloneniyaφ kis szögek és a megfelelő kis elmozdulás összege. Behelyettesítve (11) egyenlet vmestoSin. velichinui, tekintettel arra, hogy a kis szögek otkloneniyaφ. vektor silyprakticheski egybeesik x irányú elmozdulás intervallumban, de ellentétes irányú eltérés lehet írva végül visszatér (kvázi-elasztikus) erő formájában
Következésképpen a kis elhajlás szöge φ. A inga jár kvázieiasztikus erő, és ez elvégzi harmonikus rezgéseket. Találunk ilyen harmonikus rezgés időtartama matematikai inga. Erre írunk Newton második törvénye formájában skalár:
ahol α = - gyorsulás oszcillációs labdás matematikai inga vágott (13) egyenlet tömege, megkapjuk egy egyenlet formájában: = - vagy
Mivel ezeket az egyenleteket g iLvsegda pozitív érték, egymáshoz viszonyított aránya is hasonlítható a tér egy mennyiség ω 2: