Differenciálegyenletek és egyenletrendszerek
Differenciálegyenletek és egyenletrendszerek
Hogy oldja differenciálegyenletek és rendszerek MATLAB a következő ode45 funkciót (F, intervallum, X0 [, opciók]), ode23 (f, intervallum, X0 [, opciók]), ode113 (f, intervallum, X0 [, opciók]), odel5s (f, intervallum, X0 [, opciók]), ode23s (f, intervallum, X0 [, opciók]), ode23t (f, intervallum, X0 [, opciók]) és ode23tb (f, intervallum, X0 [, opciók] ).
A bemeneti paraméterek ezen funkciók közül:
- f - vektor függvény kiszámítására a jobb oldalon az egyenletek az egyenlet
- intervallum - egy sor két szám a tartományt definiáló integrációja az differenciálegyenlet vagy a rendszer;
- X0 - a vektor a kezdeti feltételeinek rendszer differenciál rendszerek
- lehetőségek - vezérlési paramétereket haladást megoldásában a differenciálegyenlet vagy a rendszer.
Minden funkció visszatér:
- tömb T - a koordinátáit rácspontok, hogy az oldatot kérik;
- X mátrix, i-edik oszlopra, amely az az érték, a vektor funkció csomópont Ti oldatok
A ode45 funkciók megvalósított eljárás Runge-Kutta 4-5 nagyságrendű pontosságot ode23 funkciókat is végre Runge-Kutta módszerrel, de a sorrend a 2-3, és a ode113 funkciót valósít Adams módszerrel.
Az M-file nevű pr 7. m write:
Ezután a parancs ablakban hívja ode113 funkció:
Az eredmény egy grafikon:
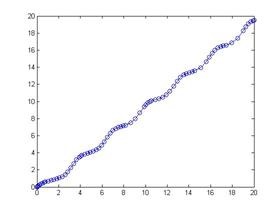
Szükséges, hogy végre egy eljárás Runge-Kutta 4 érdekében, és oldja meg a Cauchy probléma a javasolt rendszer differenciálegyenletek:
Az M-file nevű pr 8. m írás:
Ezután a parancs ablakban, hívja a óda funkció 45:
[X, y] = ode45 (@ PR8, [január 10] [0,1 0,5]);