Alapvető trigonometrikus képletek
A cikk elején, megvizsgáltuk a koncepció a trigonometrikus függvények. A fő célja a céljuk - a tanulmány alapjainak trigonometria és a tanulmányi periodikus folyamat. És trigonometrikus kört rajzoltunk semmit, mert a legtöbb esetben, a trigonometrikus függvények aránya határozza meg az oldalán egy háromszög, vagy bizonyos szegmensekben az egység kör. Azt is megemlítette, hogy kiemelten fontos a trigonometria tagadhatatlan a modern életben. De a tudomány nem áll meg, ennek eredményeként, mi is jelentősen kibővíteni a trigonometria és mozgassa a helyét a valódi, és néha a komplex számok.
Trigonometrikus képletek számos formában. Nézzük meg őket sorrendben.
Az arány a trigonometrikus függvények egy és ugyanabban a szögben
Itt érkezünk el a figyelmet az olyan fogalmak, mint az alapvető trigonometrikus azonosságok.
Trigonometrikus azonosságok - az egyenlőség, amely a trigonometrikus arányok és amely rendelkezik az összes értéke a szögek, amelyek szerepelnek benne.
Tekintsük a legfontosabb trigonometrikus azonosságok és bizonyítékot:
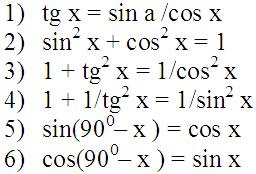
Az első identitás meghatározásából következik, az érintő.
Vegyünk hegyesszögű háromszög, amelyben van egy hegyesszögben x a Apex A.
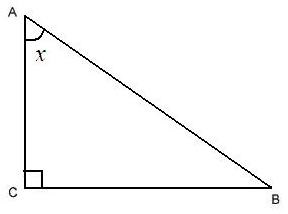
Annak bizonyítására, hogy melyek kell használni a Pitagorasz-tétel:
(VS) 2 + (CA) 2 = (AB) 2
Most osszuk el a (AB) 2 mindkét oldalon, és emlékeztetve meghatározása bűn és cos a szög, akkor kap egy második identitás:
(BC) 2 / (AB) 2 + (AC) 2 / (AB) 2 = 1
sin 2 x + cos 2 x = 1
Annak bizonyítására, a harmadik és negyedik identitások használjon korábbi bizonyítékokat.
Erre a célra, mindkét oldalán a második identitás osztva 2 cos x:
2 x sin / cos 2 x + cos 2 x / cos 2 x = 1 / cos 2 x
2 x sin / cos 2 x + 1 = 1 / cos 2 x
Alapján az első identitás tg x = sin x / cos x megkapjuk a harmadik:
1 + tg 2 x = 1 / cos 2 x
Most osztani a második személyazonosságát sin 2 x:
sin 2 x / sin x + cos 2 x 2 / sin 2 x = 1 / sin 2 x
1+ cos 2 x / sin 2 x = 1 / sin 2 x
cos 2 x / sin 2 x nem más, mint az 1 / tg x 2, így megkapjuk a személyazonosságát a negyedik:
1 + 1 / tg 2 x = 1 / sin 2 x
Itt az ideje felidézni a tétel a összege belső háromszög szögei, amely kimondja, hogy az összeg a háromszög szögeinek = 180 0. Kiderült, hogy a tetején a háromszög található a szög, amelynek nagysága 180 0-90 0-90 0 x = - x.
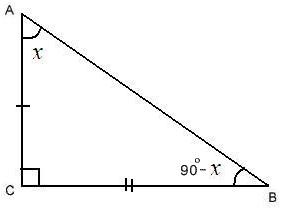
Ismét emlékszik a definíciók a bűn és a cos és kap az ötödik és hatodik identitások:
cos (90 0 - x) = (BC) / (AB)
cos (90 0 - x) = sin x
Most végre a következő:
sin (90 0 - x) = (AC) / (AB)
sin (90 0 - x) = cos X
Mint látható - minden egyszerű.
Vannak más identitások, amelyeket a megoldása matematikai identitását, hozok nekik csak formájában háttér-információkat, mert minden erednek fentiekben vizsgált.
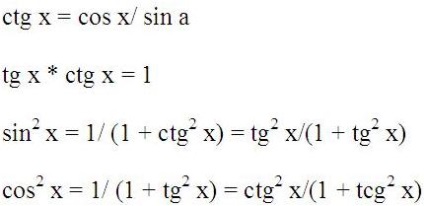
Expression trigonometrikus függvények egymás felett
(Választható jele a négyzetgyök határozza meg, amely a negyedek kör szöget?)
Majd hozzáadásával és kivonva a szögek általános képletű:
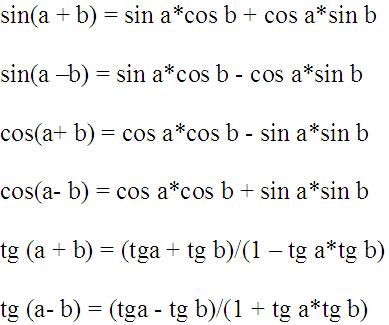
Formula kettős, hármas és fél-szögek.
Megjegyzem, hogy mindannyian erednek az előző képletek.
sin 2x = 2sin x x * cos
cos 2x = cos 2 x 2 -sin = 1-2sin x 2 x 2 x = 2cos -1
tg 2x = 2tgx / (1 - TG 2 x)
CTG 2x = (CTG 2 x - 1) / X 2stg
sin3h X = 3sin - 4sin 3 x
cos3h = 4cos 3 x - 3cos X
tg 3x = (3tgx - TG 3 x) / (1 - 3TG 2 x)
CTG 3x = (CTG 3 x - 3stg x) / (3stg 2 x - 1)
A transzformációs képletek trigonometriai kifejezések:
Egyszer, mint egy iskolás, örömmel alkalmazva a képlet a megoldás a különböző problémák, mint például a egyszerűsítése expressziója vagy egyenletet megoldani. A legfontosabb dolog, hogy - hol és milyen képlet alkalmazni kívánt, majd a többrétegű szerkezet átalakul egy közönséges numerikus kifejezés. Egy nagyon hasznos dolog a fejlődés logikus gondolkodás!
Ha az anyag hasznos volt otblagorit honlapunkon tudsz, azáltal, hogy egy adomány.
Bármilyen mennyiségű fejlesztési projekt, akkor adományoz ezen az oldalon.