Véges különbség a különböző megbízások
Véges különbség a különböző megbízások
y = f (x) jelöli
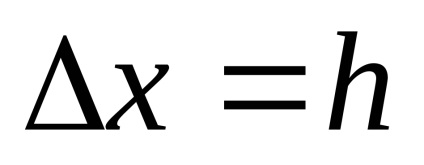
Keressük a növekmény a függvény
Úgynevezett 1. véges különbség, n-edik véges különbség a következő képlettel számoljuk:
Legyen f (x) egy polinomiális n-ed-fokú
Az ingatlan a véges különbségek:
Mi kifejezetten a véges differenciák funkciók
Legyen a függvény y = f (x) az n-edik származékot intervallumon, akkor tudjuk írni, hogy az N-edik függvény deriváltját
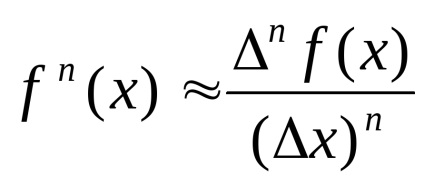
Táblázat véges differenciák
Figyelembe kell vennünk a funkció táblázatos formában, ahol
Véges különbség yi szekvencia viszonya határozza meg
Emlékezzünk binomiális tétel, tudjuk mutatni, hogy az n-edik véges differencia Yi lehet leírni, mint az összege
Ezek véges differenciák kényelmes gondoskodjon táblázatok:
Leggyakrabban a gyakorlatban használt vízszintes asztalra úgy néz ki:
Nyilatkozat közelítése problémák funkció, általános probléma a interpoláció interpoláció a legegyszerűbb feladat.
A generalizált ereje n x n a termék a tényezők az első, amely X, és minden ezt követő összetevő. H alacsonyabb, mint az előző.
X [n] - jelölést.
Találunk véges differencia az általánosított mértékben.
Nyilatkozat az interpolációs probléma
Interpoláló a legegyszerűbb feladatok a következők:
Ezeket nevezik interpolációs csomópontok, ezek a csomópontok ismert interpolációs értéke bizonyos funkciók y = f (x)
F (x) függvény az úgynevezett interpolációs.
A analitikus kifejezés f (x) nagyon összetett, vagy ismeretlen.
Geometriailag ez azt jelenti, hogy meg kell találni az y = f (x) néhány további tulajdonságokkal, különösen F (x) átmegy a ponton (xi, yi), yi = f (xi) i = 1, n
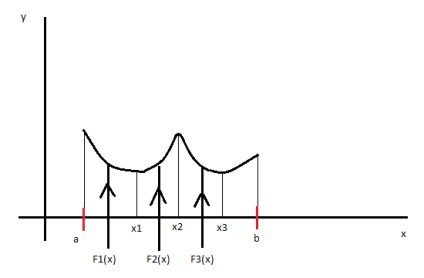
A kihívás ebben a készítményben jelen lehet egy végtelen számú megoldást.
A probléma tovább egyedileg megoldott, ha a funkció y = f (x) polinomot tekinthető y = Pn (x) foka nem nagyobb, mint n, amely kielégíti azt az állapotot Pn (xi) = yi i = 0, n.
n pontok számát. A kapott interpolációs függvény gyakran kiszámításához használt közelítő függvény értékei y = f (x) pontokban nem egybeeső interpolációs csomópontok
Ezt a műveletet nevezzük interpolációs függvény f (x).
Különbséget interpolált a szűkebb értelemben vett és széles. Ez a művelet a extrapoláció.
Először Newton interpolációs képletű (általános képlet és képletek lineáris és négyzetes interpoláció).
Tegyük fel, y = f (x) által adott pont yi = f (xi) i = 0, n, és xi = x0 + IH. h - lépése interpolációval.
Tekintsük fokú polinom y = Pn (x), amelynek a feltétel Pn (xi) = yi (1)
Feltételek (1) egyenértékű:
Kiszámítása 1. véges differencia polinom Pn (x) (lásd (2)), és feltételezzük, hogy x = x0 azt kapjuk, hogy
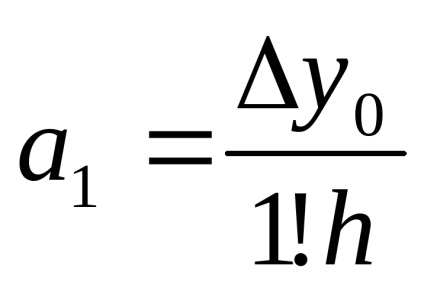
Megtalálása egy második véges különbség, és sekély, hogy x = x0
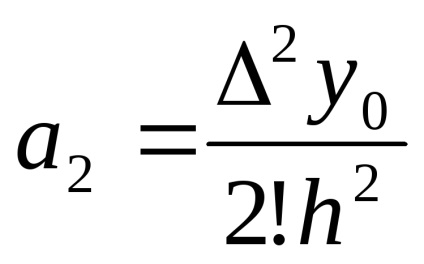
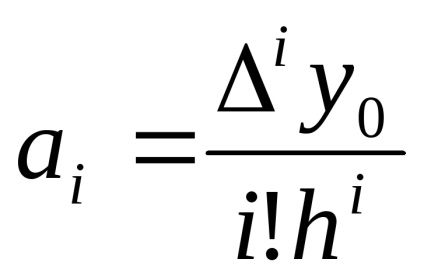
Behelyettesítve (3) egyenlet ismeretében az együttható ai. kapjuk:
- első polinom Newton.
Jellemzően az első Newton polinom írt egy sokkal kényelmesebb formában:
Általános képletű (4) kényelmetlen a gyakorlati alkalmazáshoz. Ezért a második polinom-interpoláció Newton vezette be: