Szembeni ellenállásának meghatározására logaritmikus frekvencia karakterisztika
Elmélet Az automatikus ellenőrző rendszerek
Ahhoz, hogy meghatározzuk a stabilitását Nyquist kritérium nem lehet építeni amplitúdó-fázis jellemző, logaritmikus amplitúdójú frekvencia jellemző (f. A. S.) és logaritmikus fázisban frekvenciaválasz (i. P. X.) Nyílt hurkú rendszer.
Építése L. a. x. Ez által termelt az expressziós
- Modul gyakorisága nyitott hurok átviteli függvény (6.23).
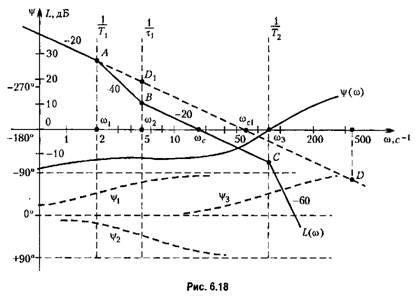
frekvencia átviteli függvény (6,23). A konstrukció l. a. x. és l. f. x. kényelmes a használata standard hálóval ábrán látható. 4.19.
A legtöbb egyszerű kialakítást kapunk, ha az átviteli függvényt a nyílt hurkú rendszer lehet csökkenteni formájában
Fázis (argumentum) a frekvencia átviteli függvény
amely megfelel a kifejezést a modul logaritmikus skálán
található na 20 dB fölött az abszcisszán.
A pont alá na 40 dB.
faktora másodrendű nevező (6,28), akkor L. a. x. izlamyvaem -40 dB / dekád, és az utóbbi lesz aszimptótát lejtőn -60 dB / dekád.
- 6 dB-lel kisebb az aszimptotikus.
Az expressziós a fázis (6,28) van a forma
(Lásd. Ábra. 6.18). Az összes többi kapunk egyszerű eltolódása a fázis jellemző, hogy a megfelelő, illeszkedő pas jelentése van egy fáziseltolódás 45 °. Meg kell figyelembe venni a jele minden idejét (6.30). Logaritmikus fázisú válasz (ábra. 6,18) úgy kapjuk meg, algebrai összegzése valamennyi a kifejezéseknek a (6.30). Építése L. f. x. Ez nagymértékben egyszerűsíthető, ha a sablon kerül előre elkészített az egyik ilyen függőség.
Hasonló szerkezetű liter. a. x. és l. f. x. lehet tenni bármilyen értéket, a különbség lesz a lejtőn az első asymptote l. a. x. és az értéke az első ciklus a kifejezés a fázis (6,27).
Az első liter. a. x.
a aszimptotikus l. a. x. módosítani kell ábra szerint. 4.15 vagy ábra. 4,16 (az első ilyen tényező figyelembe a fordított jel).
Hasonlóan a fenti építési és l. f. x. A konstrukció a komponensek a fázis jellemző, az ennek megfelelő faktort komplex gyökerek, akkor használja a grafikonok ábrán látható. 4.15.
Hivatkozva most a tanulmány a stabilitást a zárt rendszer, de épített l. a. x. és l. f. x. nyílt hurkú rendszer. Ehhez használja az utolsó szövege fölé Nyquist kritérium kapcsolódó folyosón egy. f. x. a kritikus szegmens.
. Mint korábban, az átmenetet fentről lefelé pozitívnak tekintik, és alulról felfelé - negatív.
-1 áttér a kritikus intervallumot és zárt hurkú rendszer instabil lesz.
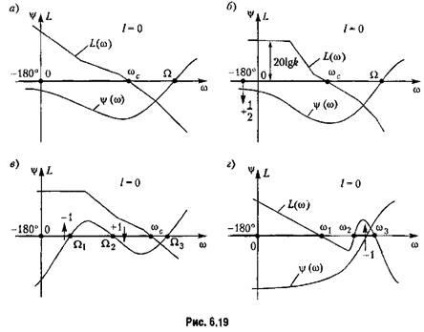
és az összeget az átmenet nulla.
Mivel -1 átmenetet a kritikus része a második szegmens, a hurok rendszer instabil.
Nagy gyakorlati előnye a Nyquist kritérium, hogy a. f. x. vagy L. h. x. nyílt hurkú képes rendszert kapunk nemcsak számítás (beleértve a használata számítógépes technológia) előre meghatározott nyílt hurkú átviteli függvény, hanem kísérletileg hozott jelenlétében a már létrehozott egy automatikus rendszer egészének vagy egyes készülékek között. Ez különösen fontos, ha a pontossága a kezdeti differenciálegyenlet, de egyik vagy másik ok kétséges.