Lecke - faktorizáció különbség n-edik hatáskörét
Rövid leírása a dokumentum:
Rövidített szorzás formula - ez egy nagyon praktikus eszköz műveletek polinomok. Általános szabály, hogy az csökkenti a komplex struktúrák polinomok egy kis kifejezi azon binomiális. Vagy, más sorrendben - a terméket a két polinom könnyen származtatható kompakt bab.
Az ilyen intézkedések szükségesek megoldásában triviális és egyenlőtlenségek, valamint a különböző bizonyítási problémákat.
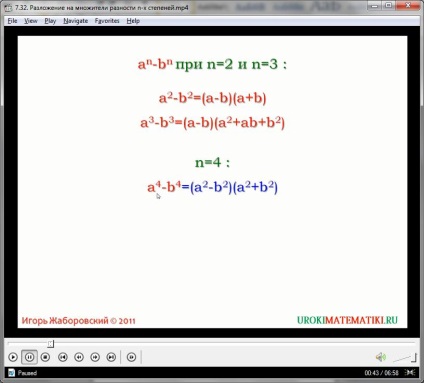
Ez a kifejezés viszonylag könnyű átalakítani, helyettesítő x 4 és 4 azonos négyzet a (X 2) 2 (y 2) 2:
x 4 - y 4 = (X 2) 2 - (y 2) 2
Ennek eredményeképpen megkapjuk a különbséget a terek, ami lehet a készülék használata FSU, mint:
(X 2) 2 - (y 2) 2 = (x 2 + y 2) (X 2 - y 2)
Másrészt, a második zárójeles kifejezésben kapott tartalmazzák különbség a négyzetek, amely könnyen átalakítható:
(X 2 + y 2) (X 2 - y 2) = (x 2 + y 2) ((x + y) (x - y))
Ebből az következik, hogy:
x 4 - y 4 = (x 2 + y 2) (x + y) (x - y)
Hagyjuk alapvető közös része (x - y), a másik két kifejezés zárójelben szaporodnak:
x 4 - y 4 = (x 2 + y 2) (x + y) (x) = (x) (x 3 + x 2 y 2 + xy + y 3)
Mit kell elosztani (x - y) később látni fogjuk. Így találtunk egy másik képlet a fokozati különbség. Ez az egyenlet elég nehéz kifejezni - de meg kell érteni, hogy ez elég logikus, hogy beleférjen számos hasonló képletek különbség meghatározásában a négyzetek és kockák. Hasonlítsa össze ezeket a képleteket egymással, ami azt találná általános minták:
x 2 - y 2 = (x - y) (x + y)
x 3 - y 3 = (x - y) (x 2 + y 2 + 2xy)
x 4 - y 4 = (x) (x 3 + x 2 y 2 + xy + y 3)
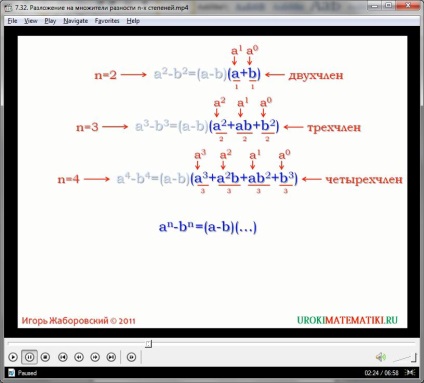
A becslést az általános képlet, amely segít átalakítani egy termék polinomok különbség változók bármilyen mértékben, fontos, hogy megértsük az általános tendenciákat az egyenletek az eredeti sorrendben. Megjegyezzük, hogy a második polinom termékünk az összege páros termékek két kifejezést. Sőt mértékben változó inverz kapcsolatot. Hogy könnyebb megérteni ezeket a mintákat, átírni egyenlet a különbség a negyedik hatványával kifejezést az alábbiak szerint:
x 4 - y 4 = (x - y) (x 3 y 0 + x 2 y 1 y 1 + x 2 + x 0 y 3)
Bármennyi a nulla energia szükségszerűen egyenlő eggyel. Ezért minden igazi változás könnyen csatolja szerkezet nulla fokos. Emlékezzünk arra is, hogy minden változó tartja - ha nincs megadva, akkor egyenlő eggyel. Ezek való bánásmód fok, és hagyjuk, hogy vezessenek be az egyenlőség érthetőbb formában.
Megjegyezzük, hogy a kifejezések száma a polinomja második zárójelben megegyezik az alapdiploma (amely változtatható a különbség). Számos polinom foka, a véleménynyilvánítás algebrailag csökken, és a mértéke a második - jön. Így a szélsőséges pontok 0 fok a legmagasabb teljesítmény kezdeti különbség kifejezéseket.
Ezekkel a megfontolások, mi származik a képlet találni a különbség az ötödik fokozat kifejezések:
x 5 - 5 Y = (x - y) (x 4, y 0 + y 1 x 3 + x 2 y 2 + x 1 + y 3 x 4 y 0)
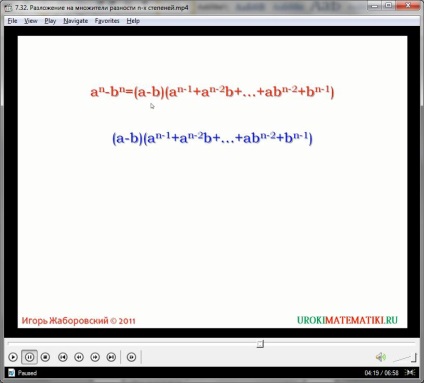
Kezdjük azzal, hogy mi tesz az első faktor (x - y) változott. A második polinom összege lesz az öt elem (a legmagasabb fokú). Elements viszont kialakult egy termék változó algebrai inverz és egymással változások mértékének. A polinom:
x 4 y 0 + y 1 x 3 + x 2 y 2 + x 1 + y 3 x y 4 0
x csökkenti a mértéke: 4: 0, y 0-ról 4. önellenőrzés hasznos tudni, hogy az összeg a fokozatok minden egytagú ebben az esetben egyenlő az összes azonos legmagasabb fokú - 5.
Továbbra is csak a helyesen írni a képletet megszabadulni a nulla fok:
X 5 - 5 y = (x) (x 4 + x 3 + x 2 y 2 y 3 + xy + y 4)
Általában, bármely mértékben n a egyenlőség:
(X) n - (Y) n = (x - y) ((x) n + (X) n-1 + ... y (Y) n - 1 + y n)
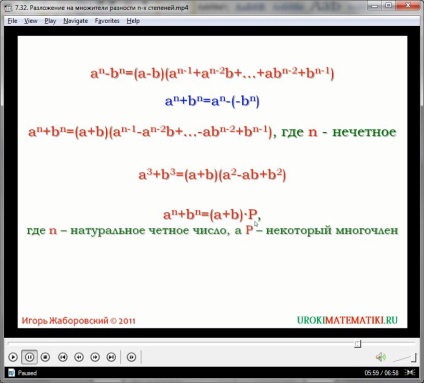
Univerzális formula megtalálása összege két kifejezés n-sósavval különbség révén származó átalakítása formájában:
x n + y n = x n - (y n)
A képlet a különbséget a kifejezések fentiekben levezetett, vezetjük le egyenletet:
x n + y n = x n - (y n) = (x + y) ((x) n-1 - (X) n-2 ... y - x (y) N - 2 + y n-1)
Tekintettel arra, hogy a tér bármely kifejezést kiküszöböli a negatív, nem tudja elképzelni, a rendelkezésre álló eszközök terek (vagy bármilyen páros fok) változók, mint a termék a két polinom.