Az üzletág a komplex számok algebrai formában

komplex szám

= X-yi nevezett konjugátum relatív kW = x + yi.

Példák a konjugátum komplex számok:

Ahhoz, hogy osztani két komplex szám algebrai formában, mint általában, amely a számláló és a nevező megszorozzuk a konjugátum nevező [1, p. 190-191].

4. példa Run osztály:

= [Szorozzuk meg a számláló és a nevező száma kettős nevező] =

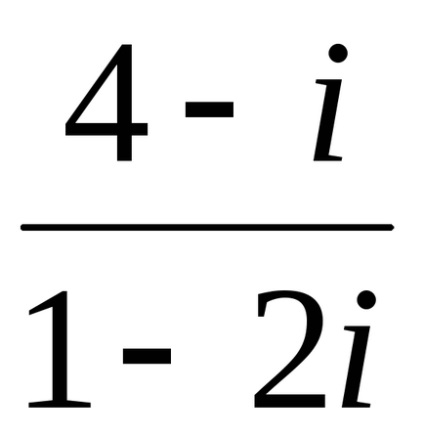
=. Megjegyezzük, hogy

Ez egy kifejezés, nem szám, így nem lehet látni, mint a válasz.

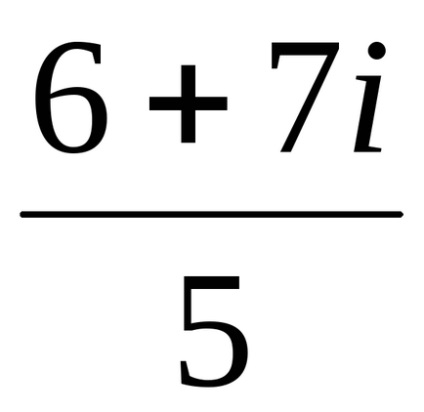
5. példa járjon:

=

=

=.

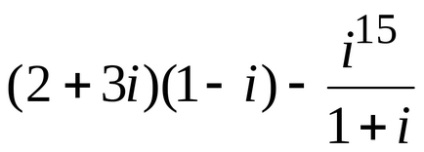
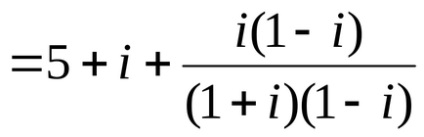
6. példa lépéseinek végrehajtására:

= [Szorozzuk meg a számláló és a nevező a frakció a konjugátumok mindkét számra nevező] =

=

=.

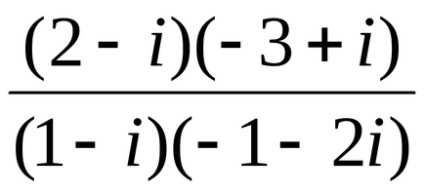
Négyzetgyöke komplex szám téglalap alakú

Definíció. komplex szám

Ez az úgynevezett négyzetgyöke komplex Vámosláz. ha[1, p. 191].

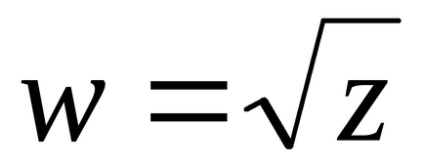
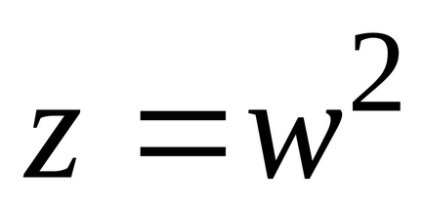
7. példa Compute

.

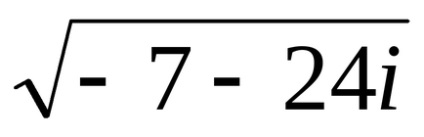
Határozat. enged

= X + yi. majd

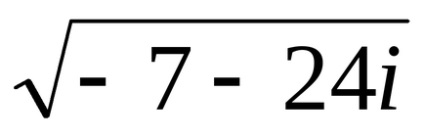
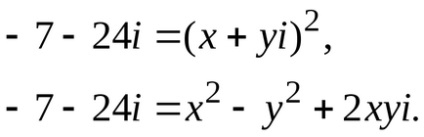
Alkotnak rendszert, egyenlő a valós és képzetes része a bal és jobb oldalán a következő egyenletet:

Mi megoldjuk külön negyedfokú egyenlet:

Egy másik lehetséges módon oldja meg a trigonometrikus formájában beadása után egy komplex szám (lásd. P. 14).

Az oldatot lineáris és másodfokú egyenlet komplex számok

A területen a komplex számok korrigálja azonos képlet az oldat lineáris és másodfokú egyenlet, mint a területen a valós számok.

9. példa egyenlet megoldásához:.

Határozat. A következő képletet találni a gyökerei másodfokú egyenlet:

10. példa: megoldani az egyenletet:.

11. példa: az egyenlet megoldásához:

.

Alkotnak rendszert, egyenlő a valós és képzetes része a bal és jobb oldalán a következő egyenletet:

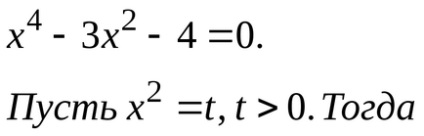
12. példa megoldására az egyenletrendszert:

Határozat. Kiterjesztjük az első egyenletből keresztül a rendszer peremennuyux peremennuyuy:

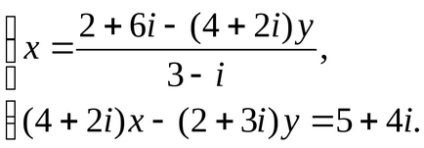
Szorozzuk meg a számláló és a nevező a frakció a konjugátum nevező:

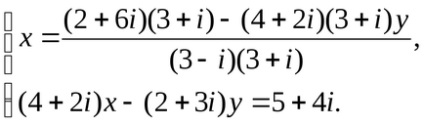
A számláló nyilvánosságra konzolok és így ezeket a feltételeket:

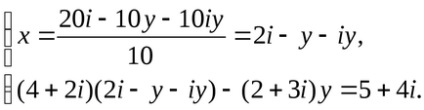
Behelyettesítve értéke x változó a második egyenletet:

;

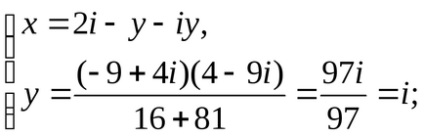
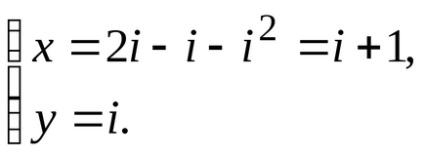
Trigonometrikus forma a komplex számok

Geometriai ábrázolása komplex számok

A tanuló tulajdonságainak komplex számok ez nagyon kényelmes azok geometriai értelmezését [1, p. 186-187]. Mivel a komplex szám meghatározása egy pár valós számok, mindegyik komplex száma Z = a + bi képviseli sík pont (x, y) koordinatamix = a és y = b. Ez a sík úgynevezett komplex síkon. abszcisszán - valós (Rez), és az ordináta tengely - képzetes tengelye (lmz).

13. példa A kilátás a gépen pontok megfelelő számok:

P

Címzés. A chislaz1 valós rész értéke -2, és a képzeletbeli - 0. Következésképpen, egy kép chislaz1 pont (-2, 0) (lásd a 1.1 ábra.).

Y szám Z2 jelentése 0 valós részt és a képzetes 3. Következésképpen, a kép chislaz2 pontjaként szolgál (0, 3). A chislaz3 valós rész értéke 1, és a képzeletbeli -4. Következésképpen, a kép chislaz3 pontjaként szolgál (1, 4).

Abban Z4 szám 1 a valós és képzeletbeli 1. Következésképpen egy kép chislaz4 pontot (1, 1).

A Z5 a valós rész egyenlő -3, és a képzeletbeli -2. Következésképpen, a kép chislaz5 pont (-3, -2).

Kapcsolódó számok képviselik pont a komplex síkban szimmetrikus valós tengelyére Rez.

Kapcsolódó cikkek

• Sűrűségének meghatározásához szilárd anyagok megfelelő formában, a tanár, hogy a tanár