Az osztás polinomok
Az általános formája egy egytagú
-egy - együttható, amely tartozhat bármely csomagja N, Z, Q, R, C
-n kitevő, amely tartozik a N készlet
Két egytagú hasonlóak, ha ugyanaz a változó és ugyanazon kitevő.
Példák: 3x -5x 2 és 2; ½x 4 és 4 2√3x
Az összeg egytagú nem hasonlít egymásra, az úgynevezett polinom (vagy polinom). Ebben az esetben a feltételek egytagú polinom. Polinom, amelynek két kifejezés, az úgynevezett binomiális (vagy binomiális).
Példa: p (x) = 3x 2 -5; h (x) = 5x-1
Polinom, amely három szempontból nevezzük trinomiális.
p (x) = egy x n + an-1 x n-1 +. 1 + a1 x + a0
ahol:
- egy, egy-1, egy-2. a1, A0 - polinom együtthatók. Ezek lehetnek természetes, egész, racionális, valós vagy komplex számok.
- egy - az együttható a kifejezés a legnagyobb kitevő (a vezető tényező)
- a0 - az együttható a kifejezés a legkisebb kitevő (lehallgatott, vagy állandó)
- N - fokú polinom
p (x) = 5x 2 -2x 3 + 7x-1
- harmadik fokozatot polinom együtthatók 5, -2, és -1, 7
- 5 - vezető együttható
- -1 - szabad távú
- X - változó
h (x) = - 2√3x 4 + ½x-4
- negyedik fokos polinom együtthatók -2√3, ½ és -4
- -2√3 - a vezető tényező
- -4 - szabad távú
- X - változó
Az osztás polinomok
Ahhoz, hogy megtalálja egy hányados, és egy fennmaradó elosztjuk p (x) q (x). akkor kell használni a következő algoritmus:- A foka p (x) nagyobbnak kell lennie, mint, vagy egyenlő q (x).
- Meg kell rögzíteni mind a polinom csökkenő mértékben. Ha p (x) nem tagja egyetlen fokozat, meg kell befejezni egy együttható 0.
- Vezető tagja p (x) van osztva egy vezető tagja q (x). és az eredmény van írva az elválasztó vonal (a nevező).
- Szorozzuk meg az eredményt minden tagjának q (x) és beírjuk az eredményt ellentétes előjelű tagjai p (x) a megfelelő hatáskörét.
- Fold termwise szempontjából ugyanolyan hatáskörökkel.
- Hozzárendelése az eredmény a többi tagjának p (x).
- Osszuk a vezető tagja a polinom kapott az első kifejezés a polinom q (x), és ismételje meg a 3-6.
- Ezt az eljárást megismételjük, amíg az újonnan kapott polinom lesz kisebb mértékű, mint a q (x). Ez a többtagú lesz való osztás maradéka.
- A polinom alatt rögzített a határvonal az osztás eredményével (hányados).
1. példa
1. lépés és a 2.) $ p (x) = x ^ 5-3x ^ 4 + 2x ^ 3 + 7x ^ 2-3x + 5 \\ q (x) = x ^ 2x + 1 $
3) x 5 4 -3x + 2x 3 + 7x 2 -3x + 5
Válasz: x 4 + 3x 2 + 2x - 8 = (x 2 - 3x) (x 2 + 3x + 12) + 38x - 8
Osztály egy polinom az első fokú
Ez a felosztás lehet végezni a fenti algoritmus, vagy még gyorsabb, ha használja Horner.
Ha f (x) = egy x n + an-1 x n-1 +. + A1 x + a0. polinom átírható f (x) = a0 + x (a1 + x (A2 +. + x (an-1 + egy x).))
q (x) - az első fokú polinom → q (x) = mx + n
Ezután a polinom különösen lesz fokú N-1.
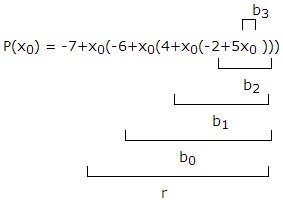
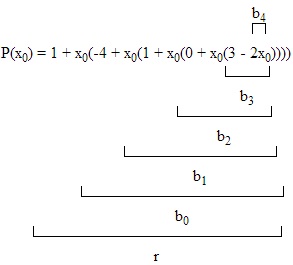
5. példa
p (x) = 3x 3 -5x 2 + 2x + 3
q (x) = 2x-1
$ X_0 = \ frac $
p (x) = 3 + x (2 + x (-5 + 3x))
b2 = 3
$ B_1 = \ frac \ cdot 3-5 = - \ frac $
$ B_0 = \ frac \ cdot \ left (- \ frac \ right) 2 = - \ frac + 2 = \ frac $
$ R = \ frac \ cdot \ frac + 3 = \ frac + 3 = \ frac \ Rightarrow c (x) = 3x ^ 2- \ fracx + \ frac $
$ \ Rightarrow 3x ^ 3,5x ^ 2 + 2x + 3 = (2x-1) (3x ^ 2 - \ fracx + \ frac) + \ frac $
következtetés
Ha elosztjuk a polinom foka nagyobb, mint egy, annak érdekében, hogy megtalálják a hányados és a maradék kell használni az algoritmus 1-9.
Ha elosztjuk a polinom első fokú mx + n. majd találni az egyensúlyt a privát és kell használni a módszert Horner $ x_0 = - \ frac $.
Ha érdekli csak a fennmaradó részlege, elegendő megállapítani, hogy p (x0).
6. példa
p (x) = - 4x 4 + 3x 3 + 5x 2 -x + 2
q (x) = x-1
x0 = 1
R = p (1) = - 4,1 + 3,1 + 5.1-1 + 2 = 5
R = 5