Szorzás és osztás a konjugátum expressziós
t. t inflexiós. inflexiós tonna. inflexiós
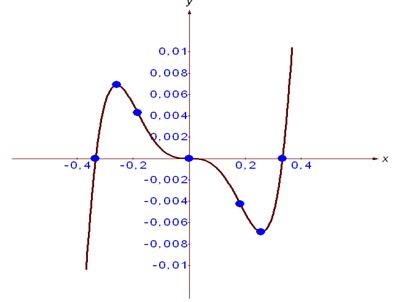
1). E (y) = (meghatározza a végén a munkát, miután rajzoló funkció).
2) a folytonosság. Aszimptota.
Ez a funkció az összes értékeket. kivéve. Mivel a függvény elemi, akkor folyamatos minden pontján saját domain. Így az egyetlen pont egy pont diszkontinuitás. Annak vizsgálatára, a természet a törés található a jobb és bal határait a függvény.
Következésképpen, a függvény végtelen pont a különbség, azaz a - pont különbség II-nd fajta. - függőleges asymptote.
Találunk a lejtőn a asymptote.
Ezért, valamint. Következésképpen, ha a menetrend függvényében, és van egy ferde asymptote.
A tartomány definíció nem szimmetrikus nulla, így a funkció sem egyenletes, sem furcsa.
4) A funkció nem periodikus.
(0, 0), (1, 0) - grafikon a metszéspontjai a koordinátatengelyek.
6) A monoton. Szélsőérték pont.
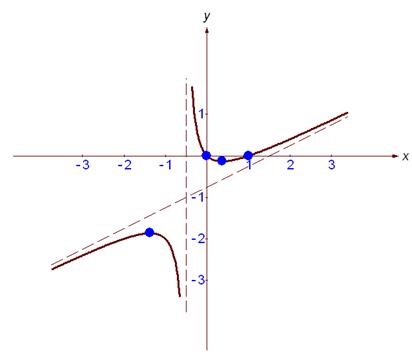
1) D (y) = R, E (y) = (meghatározza a végén a munkát, miután rajzoló funkció).
2) a folytonosság. Aszimptota.
A függvény folytonos az egész számegyenesen. Nincs törés pont. Következésképpen, nincs függőleges aszimptota.
Megvizsgáljuk a viselkedését a végén a tartományban.
Amikor. Ezért, amikor a függvény vízszintes asymptote
A tartomány definíció nem szimmetrikus nulla, így a funkció sem egyenletes, sem furcsa.
4) A funkció nem periodikus.
- a metszéspont a tengelyekkel.
6) A monoton. Szélsőértékében funkciókat.
. ha x = -2 - kritikus pont
VI. Kérdések és feladatok önálló
1. Mi a szerepe?
2. Milyen függvényt hívjuk végtelenül végtelen?
3. Mi a kapcsolat a végtelenül kicsi és végtelen nagy funkciókat?
4. Fogalmazza alapvető tételek a korlátokat.
5. Határozza meg a folyamatos működést a ponton és egy intervallum.
6. Fogalmazza szükséges és elégséges jellemzőit csökkenő (növekvő) az intervallum funkciót.
6. Az úgynevezett szélsőérték a függvény a?
7. Fogalmazzon szükséges és elégséges feltétele, hogy létezik olyan szélsőérték.
8. Határozza meg a konvexitás és konkáv görbe intervallumban.
9. Mi az úgynevezett inflexiós pontot a grafikon? Az algoritmus megtalálása az inflexiós pont.
10. Fogalmazza elegendő kritériuma az, hogy létezik egy inflexiós pont.
11. Ismertesse az általános rendszer a kutatási funkció és az építőiparban az ütemtervet.