Dil példaként hasonlósági transzformáció - studopediya
O p e n d e n n e. Hasonlósági faktor az átalakulás síkban, ahol az összes távolságok szorozva.
1. Bármely mozgása hasonlóság tényező.
2. homothety a tsentorm és együttható úgynevezett kijelző síkban, ahol minden egyes pont egy pontjának felei meg úgy, hogy.
Ellenőrizze, hogy a tágulás egy bijektív leképezés, ezért olyan átalakítása, a síkon.
Bármely két pont és képek alapján homothety van. Aztán. azaz a tágulás tényező a hasonlóság tényező.
A feltétel megkapjuk a képlet homothety
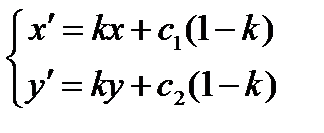
így dokazatsvoystva tágulása:
a. A homothety egyenes vonal nem halad át a közepén homothety átalakul egy sor párhuzamos hozzá, és az egyenes, amely áthalad a homothetic központ - a.
b. Dil megtartja egyszerű aránya három pontot a sorban, és ezzel megmenti a kapcsolat „hazugság között” és a szegmens fordítja vonalszakasz gerenda a sugárzási szög a sarokban.
c. Dil fordítja szöge egyenlő a szöget (miért?).
d. Dil megtartja a tájékozódás a síkon. Annak bizonyítása, ez a tulajdonság adja tágulása pontok koordinátáinak meghatározása a kép - a keret a tágulást. Aztán találunk koordinátái alapján vektorok a keretet és győződjön meg arról, hogy a meghatározója az átmenet az alapkeret az alaplappal van. azaz a referenciaértékek és az azonos irányú.
Tétel 1. Tétel (bomlik hasonlóság összetételük és homothetic mozgás) Bármely hasonlósági transzformáció leírható mint egy homothety ugyanolyan összetételű arány és mozgását.
Igazolás a h a t e l bizonyítási. Let - mint az együttható. Ha - a homothety együtthatót. majd - a dilatációs tényezővel. Ezután a készítmény egy mozgalom, és van egy - egy ötlet a hasonlóság, mint a tágulása a készítmény azonos ütemben és a mozgás.
E tételből és tulajdonságai dilatáció és a forgalmi kap tulajdonságok, mint például:
- Hasonlóság fordítja közvetlenül a sorban.
- Hasonlóság megtartja egyszerű aránya három pontot a sorban, és ezzel megmenti a kapcsolat „hazugság között” és a szegmens fordítja vonalszakasz gerenda a sugárzási szög a sarok a félsíkban félsíkra.
- Hasonlóság átalakítja szög egyenlő szögben.
- Vannak hasonlóságok az I. és II. Típusú
- A készlet minden hasonlóságok P sík egy csoportja alatt transzformációk a készítmény. Alcsoportjai E csoport: a csoport a mozgás síkjára képzett, több homothety egy közös központ, több párhuzamos fordítások és dilatációt.
- Figuryi elmondható, hogy hasonló. ha azok alapján hasonló a P csoportot hasonlóságokat. Ilyen forma például a két háromszög, megfelelő oldalain amelyek arányosak két ellipszis (két hiperbolák), amelyek különcségeit bármely két parabola.