Curves másodrendű
4.1.Kompleksnym szám kifejeződése formájában:
ahol - bármilyen valós szám, és - az úgynevezett imaginárius egység felel
A szám és az úgynevezett valós és képzetes része egy komplex szám.
Komplex számok jelentik pontokat vagy vektorok síkban a sík.
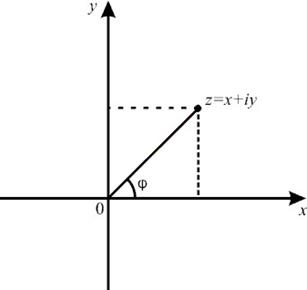
4. 2. A hossza a vektor az úgynevezett modulus komplex szám, és jelöljük. így van.
Angle. kialakítva a pozitív iránya a vektor neve argumentum egy komplex szám, és jelöljük
ahol - a legfőbb érték. meghatározott körülmények között. és
Ettől. . majd - trigonometrikus forma egy komplex szám. Euler-képlet
akkor megy a trigonometrikus és exponenciális formában
4. 3. Két komplex szám egyenlő akkor, ha azok a valós és képzetes része :; . Vagy ha a modulok egyenlő, és az érvek egyenlő vagy különböznek többszöröse:
4. 4. Alapvető műveletek komplex számok.
Ezen túlmenően, és a kivonás a komplex számok önmagukban nem adunk hozzá vagy kivonjuk a valós és a képzetes rész
Hatványozás integer):
A gyökér a komplex szám egész szám):
Root - ed-fokú tetszőleges számú különböző értékeket, amelyek csúcsainál helyezkednek el a jobb - oldalú sokszög írt kör sugara origó középpontú.
Példa. Komplex számok algebrai formában:
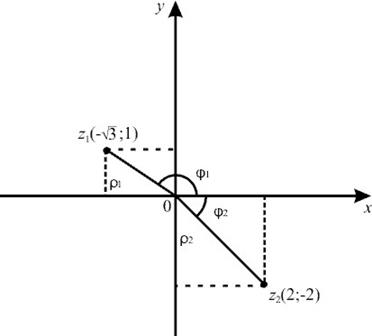
Kövesse az alábbi lépéseket :. . . . Találd meg az összes gyökereit. hogy képviselje őket a gépen.
Nézzük számát jelenti, és a komplex síkon
Az exponenciális forma :; .
Szorozzuk meg a szabály szorzás polinomok, tekintettel arra, hogy sem. (Ha megszorozzuk a fold).
Az exponenciális formában:
. (Amikor elosztjuk a levonva).
4). Jobb, ha ezt a műveletet elvégezni exponenciális formában
Megtaláljuk a gyökerei az egyenlet. .
Köbgyökét komplex szám három különböző értékeket. Ebben az esetben,
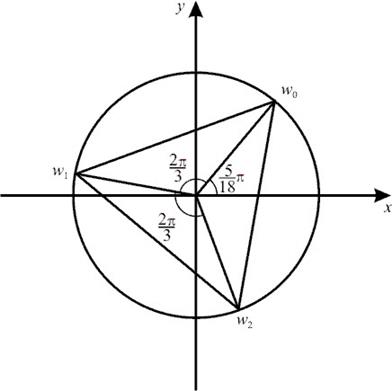
ugyanolyan modul, akkor ezek a körön origó középpontú és sugár. mivel a különbség az érveket. fekszenek a csúcsai szabályos háromszöget feliratos.