Vázlat A területek meghatározása a világon. hatálya az egyenlet. A kölcsönös elrendezése gömbök és repülőgépek. A terület a gömb. Lecke összefoglaló. Opr.okr.
Kerülete és a kör része a sík által határolt kör az úgynevezett kör. Kör nevezzük geometriai forma, amely az összes pont a síkon helyezkedik el egy előre meghatározott r távolság ezen a ponton. r - a sugár; d - átmérője Def. gömbök
Meghatározása Sphere Sphere egy felülete, amely az összes pontot a térben, található egy adott távolság (R) egy adott pont (O pont középen). Alkalmazási kör - a test eredő forgása-ness félkörben körül átmérője. T O -. A a gömb középpontján D - a gömb átmérője - szegmens összekötő bármely két pont a gömb és a középpontján átmenő. D = 2R léggömb R - a gömb sugara - összekötő szakasz bármely pontján a gömb, amelynek középpontja.
Ball test, egy szűk körben, úgynevezett labdát. Középpont, sugár és a gömb átmérője is a központja, az orsócsont és a gömb átmérője. A labda, R sugarú középső O tartalmazza az összes pontot a térben vannak elhelyezve m. A távolság nem haladja meg a R.

Történelmi információt a terület és a labda mind a „labda” és „hatályát” származik a görög szó „sfayra” - el. Az ókorban, a hatály és a labda is tisztelték. Csillagászati megfigyelések az égbolton okozta a kép egy gömb. Pythagoreusok azok félig misztikus diskurzus állította, hogy a gömb alakú égitest található egymástól bizonyos távolságban arányos időközönként a zenei skála. Ebben látták elemei világ harmóniáját. Ezért a kifejezés ment „szférák zenéje”. Arisztotelész úgy vélte, hogy a gömb alakú a legfejlettebb, azzal jellemezve, a Nap, a Föld, a Hold és az összes nemzetközi szervezetek. Azt is hitték, hogy a Föld körül egy sor koncentrikus gömbök. Gömb, Ball mindig széles körben használják különböző területeken a tudomány és a technológia. g / h kb.

Hogyan ábrázolják az irányelv hatálya alá? R 1. Jelölje meg a gömb közepén (O pont) 2. Rajzolj egy kört a központ O pont 3. megjelenítése ív látható függőleges (meridián) 4. megjelenítése láthatatlan függőleges ív 5. megjelenítése látható hori-zontally ív (párhuzamos) 6. megjelenítése láthatatlan vízszintes íven 7. magatartási a gömb sugara R O ur. env.
kör egyenlete tehát kör egyenlete a következő formában: (x - x0) 2 + (y - y0) 2 = r2 C (x0, y0) M (x, y) x y On Definiáljuk egy derékszögű koordináta-rendszer Oxy konstrukció C kör középpontú r. . C és az r sugár egy tetszőleges r távolságtól M (x, y) a TS alábbi képlettel számítottuk ki: MC = (X - x0) 2 + (y - y0) 2 MS = r. vagy MC2 = r2
Probléma 1. Ismerve a középpontjának koordinátáit C (2, -3, 0), és R = a gömb sugara 5, rekord egyenlete a gömb. Megoldás, mint az egyenlet egy gömb R sugarú, és központ a ponton (X0; y0, z0) formájában van (x-x0) 2 + (y-y 0) 2 + (Z-z0) 2 = R2, és a központ koordinálja a a gömbök (2, -3, 0), és a sugara R = 5, majd az egyenlet a gömb (X-2) 2 + (y + 3) 2 + Z2 = 25 a: (x-2) 2 + (y + 3 ) 2 + Z2 = 25 ekv. gömbök
Az egyenlet a gömb (x - x0) 2 + (y - y0) 2 + (z - z0) 2 = R2 x y z M (x; y; z) R Határozza derékszögű Oxyz koordináta-rendszer-konstrukció gömb c központ t C és. MS sugara R = (X - x0) 2 + (y - y0) 2 + (z - z0) 2 MS vagy MS2 = R. = R2 C (x0; y0, z0) így egyenlete a gömb a formája:
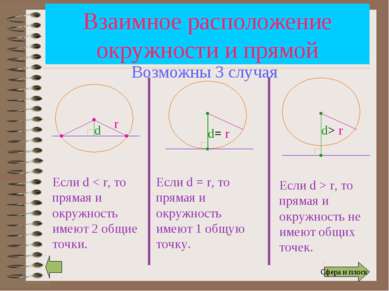
A relatív helyzete a kör és az egyenes vonal r d Ha d
Ha r d = r, akkor az egyenes vonal és a kör egy közös pont. Ha d> r, akkor az egyenes vonal és a kör diszjunktak. Vannak esetek 3 kör és lapos


Kapcsolódó cikkek