mátrix faktorizációs módszer iteratív módszer a probléma megoldására, 3d - relief helyreállítási terület
mátrix faktorizáció módszerrel
Az egyik leghatékonyabb módszer visszaállítani 3D alakja és mozgása az objektum alapuló módszer mátrix faktorizáció. Nézzük magyarázza a módszer lényege a lineáris közelítés. Fent azt mutatja, hogy a leíró egyenletek a lineáris közelítés a forma (2.3.20):
Mi képezi majd egy koordináta mérési mátrix W 2F x P mérete:

Minden sor a W mátrix tartalmazza a pontok koordinátáinak (UFP, VFP), vonatkozó adott váz a szekvencia, és mindegyik oszlop, - ugyanazokat az értékeket az adott pontokat, jelen az összes kép. Ezután az expressziós (2.3.33) átírható mátrix formában:
ahol M - mátrix mozgás (a fényképezőgép tájolása) a mérete 2F x 3, S - mátrix formában (az a pont az objektum), mérete 3 x P, T - vektor adások kamerák (kamera pozíciók térben), méretek 2F x 1, a következőképpen alakult:

Keresse meg a származási MSC a CM a tárgy pont (2.3.10):
Megjegyezzük, hogy a vektor T állíthatjuk elő összeadásával eleme egy mátrix sor-W:
akkor továbbra is működni fog a W * mátrix:
Mivel a mátrix W * jelentése a termék egy mátrix mérete M és 2F x 3 S mátrix 3 x P mérete, a rangsorban nem lehet nagyobb, mint 3. Ebben a kivitelezésben a faktorizáció mátrix rang 3 W, által termelt szinguláris mátrix bomlik (SVD):
Itt U, V - az ortogonális mátrixok, és U = diag (y1, ..., Yn), n = min (2F, P), y1, ..., yn - szinguláris értékeinek a mátrix W. érdekében minden szinguláris értékek csökkenő sorrendben, és választani a felső részmátrixának a mátrix mérete 3 x 3, amelyek értéke legfeljebb szinguláris 3. számú megfelelő a fő összetevői a mátrix W. Ezután választja a mátrixok U és V a sorok a részmátrix megfelelő három legnagyobb szinguláris értéket, megkapjuk közelítése a mátrix W. ez úgy értendő, hogy a egy ilyen bővítés nem egyedülálló, hiszen Mezhuyev mátrixok M) és S) mindig lehet beszúrni pro Intézet direkt és inverz mátrix rangja 3 Q, semmi nem változik, akkor tudjuk írni:
Itt, M és S jelenti és igaz mozgását mátrix formában.
megkapjuk a következő egyenletrendszert megtalálása becslések a mátrix Q:
Amennyiben az értékek és megfelelnek táblázat 2.3.2. (Lásd. Táblázatban az is. 2.3.1)

Ebben a papír, a rendszer (03/02/41) foglalkozott a legkisebb négyzetek (OLS) használatával SVD.
Kétértelműség alakú fellendülés szakaszában annak a ténynek köszönhető, hogy a feladat egyszerűen szimbolikus kétértelműség helyett Q mátrix az alábbi mátrix:
Orientációjának rögzítésére a tengelyek a koordináta-rendszer, például úgy, hogy kiválasztja az irányt a tengelyek ugyanaz, mint a rendszer kapcsolódó egyik kamrában, a kétértelműség az első két védjegy lehet szüntetni. Figyelembe véve összehangolás az első cellára, megkapjuk a kívánt mozgását a mátrix és a formák:
Kétértelműséget a harmadik helyen annak a ténynek köszönhető, hogy minden vettük figyelembe a lineáris közelítés, a mélység a tárgy, mint a távolság az ő gondatlansága (van egy úgynevezett „laposabbá” a jelenet). Ennek következtében, ez vezet a kétértelműség alakú fellendülés szakaszában S és a mozgás kamerák M.
Iteratív módon oldja meg a 3D-feladatok
A fő hátránya a fent említett lineáris közelítés a kétértelműséget a meghatározása a jel a mélység a helyszínre és a képtelenség kiszámítani gyújtótávolság a kamerák. Elérhetőség Képek perspektivikus torzítás további információforrást, hogy megszüntesse ezeket a hiányosságokat.
Mivel a módszer pontos, le van írva uravneiyami (03/02/39), amelyben rakjuk g állandó a kereteket.
például a már találkozott helyére ZF ZF „újraírás (2.3.44):
Így a jobb oldalon a egyenletek kapott megfelel a jobb oldalon a egyenletek a MOSFET (2.3.17), és a bal az összege a bal oldali részén a lineáris közelítések és adalékok. A mátrix formában most kapjuk:

Ie W mátrix képviseli két kifejezést, amelyek közül az első, W1, megfelel a megadott mérés előtt mátrix és a második, W2, függ W1, SP, KF, és van értelme, korrekció perspektivikus torzulások:
Amint azt korábban kimutatták a rangot a jobb oldalon (2.3.45) mindig egyenlő 3, azt javasolják, hogy válassza ismétléseket paraméter b valamely ismert az előző lépésben érték sp, kf, oly módon, hogy megőrizzék az egyenlőség a soraiban a két rész (02/03/45). Így, az egyenletrendszert (2.3.45) lehet megoldani iteratív, tisztázva korrekciós mátrix.
Javasolt iteratív algoritmus jól működik az esetben, ha a központi irányítás az objektum annak a ténynek köszönhető, hogy első megközelítésben választott MOS - vetítés. Ha van jelentős igény dolgozni szigorúan egy olyan helyzetben, nem központi irányítást, akkor jobb, ha a 42
kezdeti közelítését paraperspektivnuyu vetítés. Megfogalmazzuk a javasolt algoritmus nemlineáris rekonstrukciós probléma.
1. Feltételezzük, a (2.3.46) száma iteráció q = 0, a paraméter S = 0, W (0): = W1, W2 (0): = 0.
2. Oldjuk meg a rendszert leíró egyenletek MOS megközelítés:
3. Hisszük most: q: = q + 1.
4. Számítsuk korrekciós mátrix:
5. Mi találtunk az együttható b (q) választotta őt, mint a rangot a W mátrix (q) egyenlő marad 3, ez kell keresni:
ahol y1, y4 - ez az első és a negyedik szinguláris érték mátrix W (q). A variációs tartomány a paraméter b (q) határozzuk meg a feltétel:
6. Frissítse a mátrix
7. A 2. lépés, ha nem elégedett kilépési feltétel:
ahol e értéke választjuk elegendően kicsi.
8. egyértelműség mélység jel jelenet:
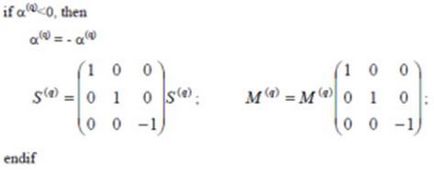
9. Önterülő MSC által SC társított egyik kamrába.