A képlet a Lorentz-erő a fizika
Force. ható egy mozgó töltött részecske olyan mágneses mezőben, amely egyenlő:
úgynevezett Lorentz-erő (mágneses erő).
Kezdve a meghatározás (1) a modul vizsgált erőssége:
ahol - a részecske sebességvektor, q - felelős a részecske, - a mágneses indukció vektor a területen egy olyan ponton töltés található, - közötti szög a vektorok és a. Tól (2) az következik, hogy ha a töltés mozog párhuzamos erővonalai a mágneses mező, a Lorentz-erő nulla. Előfordul, hogy a Lorentz-erő megpróbálja azonosítani, kijelöli, a kód:
Az irány az Lorentz-erő
Lorentz-erő (valamint minden teljesítmény) - ez egy olyan vektor. A irány merőleges a sebesség vektor és a vektort (azaz, merőlegesen arra a síkra, amely vektorok a mágneses indukció és a sebesség), és a jobb oldali szabály által meghatározott szabály (jobbmenetes csavar) Fig.1 (a). Ha van dolgunk negatív töltés, a Lorentz-erő tonapravlenie ellenkező eredményt vektort terméket (1. ábra (b)).
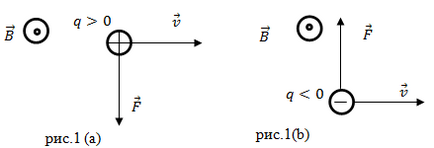
vektor merőleges a síkra a rajzok számunkra.
A vizsgálat tulajdonságait Lorentz-erő
Mivel a Lorentz-erő mindig merőleges a sebesség a díj, a munkáját a részecske nulla. Kiderült, hogy az eljáró egy töltött részecske útján állandó mágneses tér nem tudja megváltoztatni az energiát.
Ha a mágneses mező egységes és merőleges sebességét a töltött részecske, a töltés hatása alatt a Lorentz-erők fogja mozgatni a sugara R = const kerülete olyan síkban, amely merőleges a vektor a mágneses indukció. A kör sugara egyenlő:
ahol m - részecske tömege, | Q | - részecske töltés egység, - a Lorentz relativisztikus tényező, c - a fénysebesség vákuumban.
Lorentz-erő - ez a centripetális erő. Az irányt elemi töltött részecskéket tartalmazó mágneses mező eltérést megkötésére annak jele (2. ábra).
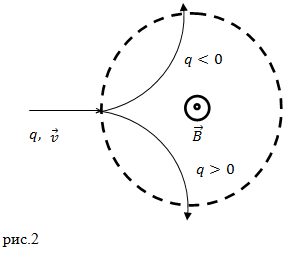
A képlet a Lorentz-féle erő jelenlétében a mágneses és elektromos mezők
Amikor egy töltött részecske mozog a térben, amelyben egyidejűleg két mezőt (mágneses vagy elektromos), az erő, amely hat rá, van:
ahol - az elektromos mező vektort egy olyan ponton, ahol a töltés található. Expression (4) kapunk empirikusan Lorentz. Az az erő, amely előfordul a (4) képletű is nevezik a Lorentz-erő (a Lorentz-erő). A szétválás a Lorentz-erő a komponensek: az elektromos és mágneses relatív, mivel ez összekapcsolódik a választott inerciális referencia rendszer. Például, ha a referencia-képkocka fog mozogni a ugyanolyan sebességgel, mint a töltés egy ilyen rendszerben, a ható Lorentz-erő a részecske nulla.
Mértékegységek a Lorentz-erő
Az alapvető mértékegysége a Lorentz-erő (vagy bármely más erő) SI egységekben van: [F] = H
Példák problémák megoldása
Feladat. Mi a szögsebesség az elektron, ami mozog egy kör egy mágneses mező indukció B?
Határozat. Mivel az elektron (egy részecske, amelynek töltése) elvégzi a mozgását a mágneses térben, akkor működteti a Lorentz-erő a formában:
ahol q = qe - az elektron töltése. Mivel ez a feltétel azt mondta, hogy az elektron mozog egy kört, akkor az azt jelenti, hogy ezért a kifejezés a Lorentz-erő a modul formájában:
Az erő Lorentsayavlyaetsya centripetális és emellett a Newton második törvénye lesz a mi esetünkben egyenlő:
Mi egyenlőségjelet tesznek a jobb oldalán a kifejezést (1.2) és (1.3), van:
A kifejezést (1.3) megkapjuk a sebességet:
elektron keringési ideje kerülete körül lehet meghatározni:
Ismerve az időt, megtalálja a szögsebesség, mint:
Feladat. A töltött részecske (töltés q, a tömeg m) olyan sebességgel vvletaet olyan régióban, ahol egy elektromos tér intenzitása E és a mágneses mező indukciós B. Vektorok és ugyanabban az irányban. Mi a gyorsulás a részecske momentnachalaperemescheniya a mezőket, ha?
Határozat. Készíts egy rajzot.
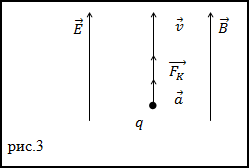
Egy töltött részecske Lorentz-erő:
A mágneses komponens merőleges irányban a sebesség vektor (), és a mágneses indukció vektor (). Elektromos komponens kollineáris a vektorral az intenzitás () elektromos mező. Összhangban a második törvénye Newton, van:
Azt látjuk, hogy a gyorsulás egyenlő:
Ha a töltés sebessége vektorok párhuzamos majd. kapjuk: