Aszimptota a grafikonon - studopediya
Meghatározása .Asimptotoy a görbe egy egyenes vonal, amely távolság a pont a görbén nullához közelít végtelen távolságra a kezdőpont a görbe, azaz a .
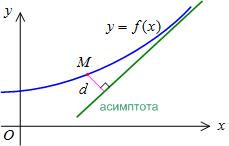
Aszimptota lehet függőleges, vízszintes és ferde.
Közvetlenül függőleges asymptote. ha
Ahhoz, hogy megtalálja a függőleges aszimptóta kell találni azokat az értékeket. amelynél a funkció növeli vagy csökkenti korlátlanul. Általában ez a második fajta törés pont.
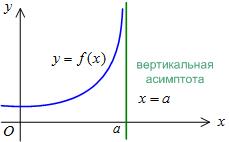
Példa 1. Keresse meg a függőleges aszimptotáját a grafikon funkciók.
Határozat. A nevező nulla lesz a pont. Mivel mind. Ezért, a közvetlen és függőleges aszimptotákkal.
Közvetlenül a vízszintes asymptote. if.
Ahhoz, hogy megtalálja a vízszintes asymptote meg kell találni a határ a funkció és.
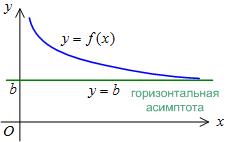
Példa 2. Keresse meg a vízszintes aszimptotáját a grafikonon.
Határozat. Találunk a határ. Következésképpen, a vízszintes aszimptóta (és balra) a grafikon az ezt a funkciót egy egyenes vonal. Megjegyezzük, hogy. Ezért a vízszintes aszimptotáját a jog nem létezik.
Egyenletben ferde aszimptotákkal formájában van,
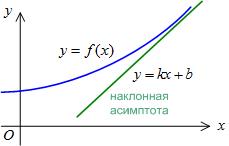
Példa 3. Keresse meg a lejtőn a aszimptotáját a grafikonon.
Határozat. Találunk a szögletes együtthatója asymptote :.
Ezután kiszámítjuk a szabad kifejezés a asymptote egyenlet:
Így, a lejtőn a aszimptotáját grafikonja ez a funkció egy egyenes vonal.
Kérdésre. Vízszintes aszimptotájának a grafikon egy egyenes vonal