Amellett, tápszerek alapvető trigonometrikus függvények
A képletek mellett használják, hogy kifejezzék a szinuszok és koszinuszokat az A és B szögek, az értékek a függvények cos (a + b), COS (a-b), sin (a + b), sin (a-b).
Ezenkívül képletek szinusz és koszinusz
Tétel: Bármilyen a és b, a következő egyenlőség cos (a + b) = cos (a) * cos (b) - sin (a) * sin (b).
Belátjuk ez a tétel. Tekintsük a következő kép:
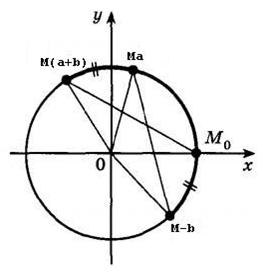
Rajta van, a pontok Ma, M-b, M (a + b), kapott elforgatásával a pont Mo szögben egy, -B, és a + b, ill. A meghatározások szinusz és koszinusz koordinálja ezeket a pontokat sleyuuyuschimi: Ma (cos (a) sin (a) pont), Mb (cos (-b); sin (-b)), M (a + b) (cos (a + b); sin (a + b)). UgolMoOM (a + b) = ugolM-Boma tehát egyenlő háromszögek MOOM (a + b) és M-BOMA, ahol ezek egyenlő szárú. Ez azt jelenti, hogy egyenlő és bázis MoM (a-b) és M-BMA. Ezért (MOM (a-b)) ^ 2 = (M-BMA) ^ 2. A képlet a két pont közötti távolság, kapjuk:
(1 - cos (a + b)) ^ 2 + (sin (a + b)) ^ 2 = (cos (-B) - cos (a)) ^ 2 + (sin (-B) - sin (a) ) ^ 2.
sin (-a) = -sin (a) és cos (-a) = cos (a). Mi átalakítják egyenlőség ezek a képletek és a tér az összeg és a különbség, akkor:
1 -2 * cos (a + b) + (cos (a + b)) ^ 2 + (sin (a + b)) ^ 2 = (cos (b)) ^ 2 - 2 * cos (b) * cos (a) + (cos (a) ^ 2 + (sin (b)) ^ 2 + 2 * sin (b) * sin (a) + (sin (a)) ^ 2.
Most kell alkalmazni Pitagorasz-trigonometrikus azonosság:
2-2 * cos (a + b) = 2 - 2 * cos (a) * cos (b) + 2 * sin (a) * sin (b).
Itt mi tetszik, és csökkenti -2:
cos (a + b) = cos (a) * cos (b) - sin (a) * sin (b). QED.
Tartsa a következő képlet szerint:
Ezek a képletek lehet beszerezni a fent említett, a következő képlet segítségével és cseréje működtető ab -b. A tangens és kotangens is vannak hozzáadásával képlet, de nem igaz az összes érvet.
Ezenkívül képletek érintő és kotangens
Bármely szögek a, b kivéve a = pi / 2 + pi * k, b = pi / 2 + pi * n, és a + b = pi / 2 + pi * m, minden egész szám, k, n, m lesz a következő képlet:
tg (a + b) = (tg (a) + tg (b)) / (1-tg (a) * tg (b)).
Bármely szögek a, b kivéve a = pi / 2 + pi * k, b = pi / 2 + pi * n, és az a-b = pi / 2 + pi * m, minden egész szám, k, n, m lesz a következő képlet:
Minden szögek a, b kivéve a = pi * k, b = pi * n, a + b = pi * m és bármely egész szám, k, n, m jelentése a következő képlet:
CTG (a + b) = (CTG (a) * CTG (b) -1) / (CTG (b) + CTG (a)).
Minden szögek a, b kivéve a = pi * k, b = pi * n, A-B = pi * m és bármely egész szám, k, n, mbudet a következő képlet:
CTG (a-b) = (CTG (a) * CTG (b) +1) / (CTG (b) -ctg (a)).