irányított gráf
Vannak jelentős csoportjára gyakorlati problémákat kell megoldani a segítségével grafikonokat tartották lehetségesnek. Gépjárművezető és terek a város által képviselt sík gráf. De ha ez a rendszer használatához szükséges céljából az utazás a város és a forgalom bizonyos utcák egyirányú. Akkor is Betájolhatom nyilak található, közvetlenül a széleit.
Él gráf irányított, ha az egyik csúcsa tartják az elején, a másik végét a bordák.
Count az összes amelynek szélei vannak irányítva, az úgynevezett irányított gráf.
A bordák irányított gráf bizonyos fix elején és végén nevezik ívek. Vi Vj ¹ Vj Vi
Half-bemeneti vertex irányított gráf élek számát, amelyre ez a vég csúcs. Jele: deg + (V)
Half-kimeneti csúcsok egy irányított gráf az élek számát, amelyre ez a csomópont a kezdet. Jele: deg - (V)
A digráf irányított út az úgynevezett utat.
Nem él utat kell kétszer ülésezik, és az irányt mindegyik ív egybe kell esnie a útvonalában.
Pathway - egy rendezett élek irányított gráf, amelyben a végén az előző élre egybeesik az elején a következő, és minden él egyedülálló.
# 8204; # 8204; # 8204; # 8204; # 8204; # 8204; | # 8204; BP | = 3
Ha egy irányított gráf nem „pass” a felső, a tetejére a másik, a köztük lévő távolság az úgynevezett végtelen.
A tetején egy irányított gráf nevezzük forrást. ha az nem tartalmaz semmilyen egy ív, azaz d + (v) = 0.
A tetején egy irányított gráf nevezzük lefolyás. ez nem jön ki minden ív, azaz d- (v) = 0.
A szomszédsági mátrix - egy négyzetes mátrix n dimenziós * n, (ahol n a csúcsok száma) egyedileg képviselő felépítését.
A =, i, j = 1,2. n, és minden eleme a mátrix a következőképpen definiálható:
aij = 1, ha ∃ ív (Vi, Vj),
aij = 0, ha nincs ív (Vi, Vj).
Metszéspontjában az oszlop és a szennyvíz kerül 1 vagy 0 függően. ha van egy ív, hogy megy a vonal címke címke oszlopban.
előfordulási mátrix sorok felelnek meg a csúcsok és az oszlopok - az élek vagy ívek.
Mátrix esetén digráf G - a mátrix B = (bij) n × m, hogy
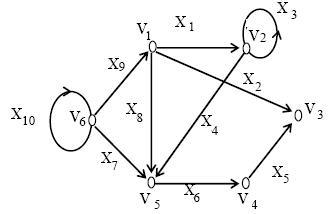
Hagyja, vi és vj - a tetején a digráf G. A felső Vidostizhima a Vj. ha van (Vi, y) -path. Bármely csúcspont elérhető magából. A csúcsok vi és vj szorosan összefüggnek, ha azok elérhetők egymástól.
Például, az ábrán bemutatott grafikont 25,2, a csúcsok V2 és V3 erősen csatolt, a csúcsok V1 és V4 erősen csatolt, a vertex V6 elérhető a V1. de elérhetetlen távolságra vertex V1 V6.
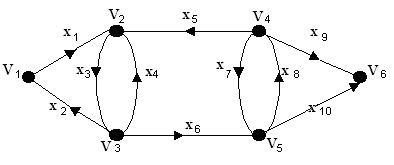
Erősen összefüggő komponens egy gráf erősen összefüggő részgráf ez, nem a tulajdona más részgráfot erősen összefüggő részgráfja G-orientált.
A grafikon az ábrán látható. 25.3 három erősen összefüggő komponensek. Ezek körül szaggatott vonalak.
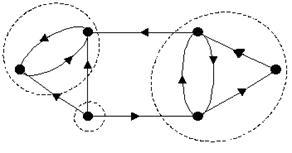
Vegye figyelembe, hogy kedvéért az nem tartozik az egyik összetevője erős kapcsolat.
Hatósugár leírása a oszlopmátrix elérhetőségi R = [rij], i, j = 1, 2 n, ahol n - a csúcsok száma, és az egyes elemek a következőképpen határozzuk meg:
rij = 1, ha xj csúcs megközelíthető x i,
rij = 0, egyébként.
Kontrdostizhimosti mátrix Q = [qij], i, j = 1, 2 n, ahol n - a csúcsok száma, meghatározása a következő:
qij = 1, ha xj a csúcsok érhető vertex xi,
qij = 0, egyébként.
Mátrix orientált erősen összefüggő gráf D - négyzet mátrixot S (D) = [sij] n-edrendű. elemei, amelyek