Rövid elméleti információk - studopediya
Optimization - céltudatos tevékenység. hogy a legjobb eredményeket érje megfelelő körülmények között.
Jellemzően az optimalizált érték összefüggésben van a működés hatékonyságát az objektum. Általában a tárgy lehet tekinteni minden olyan ipari komplexum: a berendezés, szerelés, bolt, gyár, üzem, ipar. Optimális, vagy a legjobb, a munkamódszer a mérendő tárgy, mint egy kvantitatív mérőeszközt - optimalitási kritériumként.
Optimalitás kritérium - mennyiségi értékelését optimalizált minőség. Ez a fő tünete ítélt, milyen a rendszer működését, ez a folyamat működik, milyen jól optimalizálási probléma megoldódott.
A készítmény az optimalizálási probléma eltérő lehet attól függően, hogy az elérni kívánt célokkal az általános beállítás onazaklyuchaetsya meghatározásakor az értékeket a kontroll paramétereit. optimalizálása elfogadott minőségi mutató - optimum kritériumnak. amelynek maximális vagy minimális lehetséges értéke, azzal a megkötéssel, hogy az alábbi korlátozások változók. által kivetett technológiai, működési, szerkezeti követelményeknek, a stabilitás, a sávszélesség, a nyersanyagok hozzáférhetősége és így tovább. n.
1) statikus optimalizálási probléma a folyamatok játszódnak le az egyensúlyi állapot, amely dönt a létrehozása és végrehajtása az optimális modell a folyamatot;
2) a dinamikus optimalizálási probléma vagy feladat létrehozása és végrehajtása az optimális folyamatirányítás alatt átmeneti üzemi körülmények között a rendszer megoldásokat igénylő dinamikájának vizsgálata a folyamat (például, start-up folyamat vagy át az egyik üzemmódból a másik minimális eltérése a termék minősége, az optimális szabályozás szakaszos eljárás ).
Hogy oldja meg optimalizálási problémák szükséges:
1. Hozzon létre egy matematikai optimalizációs modell a tárgy;
2. Jelölje optimalitási kritériumként, és alkotnak egy célfüggvény (célfüggvény lehetnek korlátozás nélkül és korlátozások bizonyos paraméterek);
3. Adjuk vezérlő paraméterek és azok esetleges korlátozásokat;
4. Válassza ki és hajtsanak végre egy eljárás optimalizálása, amely lehetővé teszi, hogy megtalálja szélső értékei az ismeretlen mennyiségek.
Az eljárás megoldására az optimalizálási probléma magában létrehozó folyamatok (vagy választott) az ellenőrzési paraméterek (tényezők) és azok mennyiségét. az képes megváltoztatni, amely lehetővé teszi, hogy szabályozza és optimalizálja a folyamat (amely lehet a hőmérséklet, nyomás, idő, összetétele a kiindulási keverék és mások.).
A többi paraméter ebben az esetben nem szabályozott, de az értékek meghatározása során figyelembe az optimális feltételeket.
Miután megadott paramétereit. a legtöbb optimalizálási problémák határt szabnak a variációs tartomány ezen paraméterek (változók).
Korlátozások - technológiai értékek, amelyek a folyamat a készülék működését (az egység) belül kell lennie az előírt tűréshatárok technológiát.
Osztja az egyenlőség és az egyenlőtlenség korlátokat típusát. egyenlőség korlátok létre egy bizonyos paraméter értékét
hi paraméter lehet tekinteni, mint az egyik bemenet szabályozott szabályozatlan (alapanyag összetétele, méretek, stb eszközök. d.)
egyenlőtlenség Típuskorlátozások meghatározzák, amelynél a megengedett paraméterei változásának a folyamat X
Minden módszer megoldására optimalizálási problémák sorolhatók az alábbi fő csoportokba.
1. Analitikai módszerek. Hozzá vannak szokva, amikor tudjuk különböztetni a célfüggvény és megtalálja a szélsőséges.
2. Módszerek matematikai programozás (lineáris, dinamikus, nem-lineáris). Mert azok használatáról kell kiszámítható célfüggvény: lenni ismert algoritmus, amely lehetővé teszi, hogy az A értékét optimalitási kritériumként adott értékeknél tényező.
3. Módszerek véletlenszerű keresés (kísérleti optimalizálás). alkalmazható, amennyiben az a fajta a célfüggvény ismeretlen. Ezután végezzük el a tervezés és a végrehajtás a kísérlet, hogy ennek eredményeként, hogy elérjék az optimális terület.
Ismertek továbbá a hibrid módszerek, amelyek egyesítik néhány előnye az egyes módszerek a különböző csoportok.
Keresés optimális numerikus módszerek. A lényege numerikus módszerek: száma számított értékei F különböző értékeket az érvelés; Összehasonlítása ezen értékek megmutatja, milyen irányba mozog a térben tényező megközelíteni az optimális.
1. optimalizálása brute force akkor alkalmazzuk, ha a számos lehetőség természetesen. Számított célfüggvény minden lehetséges opciókat, és válassza ki a legnagyobb (vagy legalábbis) értéket.
2. vizsgálat - módszer közel a válogatás, de alkalmazható egy folytonos függvény.
Vegyük például egy egydimenziós vizsgálat - az eset, amikor keres egy maximum célfüggvény tényezővel (a minimális keresést végezni azonos módon).
Mi határozza meg a szórási tartományt X faktor a-ból b. Itt a és b - korlátozásokat, amelyek lehet állítani bármilyen valós probléma.
Ez [a, b], amely azt fogja keresni extrémuma a célfüggvény hívják a bizonytalansági intervallum. A feladat megtalálni a szélsőérték csökken szűkületben bizonytalansági intervallumot. az alábbiak szerint (lásd 1. ábra) úgy érjük el, szkennelés:
Úgy döntünk értéke q - száma célfüggvényértékek, ami kell számolni. Kiszámítjuk az intervallum # 916; s
Elhalasztja pontból a B pont időközönként # 916; s (1. ábra). A határokat az egyes intervallumok nevezik csomópontok; az 1. ábrán, minden egyes csomópont - kereszt jelöli.
a, b - a határokat a bizonytalansági intervallum.
1. ábra - Menetrend kutatás szkennelési funkció:
Minden egyes csomópont rassschitaem F (x) (lásd. A lényeg ábrán. 1.). Most, hogy legfeljebb a nagyobb kapott értékek - az ábrán a 4. pont a bal oldalon. Végére a számítás intervallum bizonytalanság # 948; Márka 2 # 916; s: igaz max eshet sem jobbra, vagy balra a pont szerzés a legjobb (szaggatott vonal az 1. ábrán).
A képlet határozza meg a módszer hatékonyságát
Módszerek az irányított keresés. Módszerek irányított keresés hatékonyabb, de nem rendelkeznek a sokoldalúság, amely különbözik a szkennelést. Ezek hatékonysága abból ered, hogy a haladás a tényező térben történik az irányt a kívánt szélsőséges. De a keresés irányát a következő alapvető követelmények - a feltétele unimodális funkciói, vagyis funkciót engedélyezni kell a területen csak egy szélsőérték kívánt karakter (egy maximum, ha keres egy maximum egy legalább az ellenkező eset).
Amikor kiválasztja a keresési módszer szélsőérték két fő esetben: 1) F attól függ, csak az egyik tényező, F = F (x): akkor beszéljünk az egydimenziós keresés; 2) több tényező - a többdimenziós keresést. Tekintsünk egy egydimenziós keresési módszer (eljárás dichotómiák), valamint három - többdimenziós - koordináta származású, gradiens módszer, véletlenszerű keresési módszert.
A kettősség. Ahogy a leírásban a szkennelés, úgy a keresés a maximális intervallumban [a, b], a 2. ábrán látható.
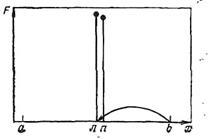
2. ábra - Keresés tartás maximális dichotómiák.
Elosztjuk az intervallum fél - l pont (balra) az ábrán. Mi az A értékét F = F (L) ezen a ponton. Válassz egy kis értékkel tényezője # 949;. és szállít a szegmens megfelelő pontot n = l + # 949;. Kiszámítjuk F (n). Mivel F (n)> F (n), amint a 2. ábrán látható, azt lehet mondani, hogy ha F (x) unimodális, akkor a maximum a bal fele a szegmens.
Dobja a jobb fele a szegmens (az egyik a maximális nem). Erre jobb szélén - b pont - költözik egy pont L. A lényeg L jelöli b .A 2. ábra, ez a transzfer jelöli egy nyíl. (Természetesen, ha lenne F (l) Miután a megfelelő szegmenshatáron átadásra, a feladat vissza az eredeti feltételeknek megfelelően intervallum B-be, amelynek meg kell találni a legnagyobb. Ezért az alábbi számítást hajtjuk végre ciklust, nem különbözik az előzőtől, kivéve a B érték. Ilyen algoritmust (számítási áll azonos munkafolyamaton, különböző csak a kezdeti feltételek) nevezzük egy iterációs. Megáll az iteráció, ha a bizonytalansági intervallum kisebb, mint a # 949; : A hatásosságot a kettősség algoritmus a következőképpen definiálható: az egyes pár számítások (és pont L n) csökkenti a [a, b] kétszer. Jelöljük a kezdeti szegmense az index ref. Ha ezt a számítást q (q - még), akkor Koordinátor származású. Válogatott koordinátáit a kiindulási pont a keresési h1n és 2N. egységenként növekvő mindkét tényező (lépések) H1 és H2. és kis lépésekben tényező # 949; 1 és # 949; 2. Számított érték F (h1n. CnH2n) 1 (3. ábra). Továbbá, anélkül, hogy megváltoztatná az értéke x2, elkezdjük mozgatni a tengely mentén x1, így minden egyes lépésében ez a tényező növekmény H1 (vagy -H1. Attól függően, hogy vezetés közben, hogy milyen irányba F növekedés fog bekövetkezni). Minden lépésnél, - a 2., 3., 4., stb - elvégzett számítás F. lépéseket folytatni, amíg a növekedés folytatódik F. sikertelen feltesszük azokat a lépéseket, amelyek kaptak a minimális értéket az F, mint az előző; Az ábrán vannak jelölve kereszt. Miután az első sikertelen lépés (6 pont) visszatérhet az előző pontban (ebben az esetben - a fenti 5. pont), fix értéke x1 és x2 kezdenek változtatni, ami neki H2 vagy-H2 növekmény (a 7., 8., 9., 10.).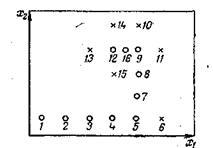
A - sikeres lépéseket; x - sikertelen lépéseket.
3. ábra diagramja mozgás a térben tényező az optimalizálás
A módszer koordináta származású
Ezután ismét mozog a tengely mentén x1 (pont 11, 12, 13), ismét a változó irányban (14., 15.), stb 3. ábra egy olyan helyzetben, amikor a 12 pont mozogni sehol: .. Az a környező pont (9, 13 , 14, 15), a F érték kisebb, mint ez a. Ez azt jelenti, hogy már elérte a maximális és a korábbi nagy lépésre 12 pont minket rajta. Ezért csökkenteni lépéseket (például felére - egy pont 16 cm). És továbbra is keresni a csökkentett lépéseket. lépésben redukció végezhető többször. De amikor kisebb lépésekben kevesebb, mint megfelelő # 949; 1 és # 949; 2. Úgy vélik, hogy a legnagyobb feljegyzett elég pontosan, és akkor befejezi a számítással, a legjobb pont az optimális.
gradiens módszer létezik számos lehetőséget. Vegyük az egyik legegyszerűbb.
Mi választjuk ki a referenciapont koordinátái h1n és 2N. lépéseket H1 és H2, és kis lépésekben # 949; 1 és # 949; 2. Mozgás az optimális kezdete nem mentén bármilyen koordináta tengelyt és az irányt a gradiens a célfüggvény (vagy, látszó legalább a gradiens az ellenkező irányba). Mivel H1 és H2 vett egységnyi növekedéséhez koordinátákat, a gradiens képlet kap a formában:
Kiszámításához a gradiens iránya parciális deriváltjai a célfüggvény a tényezők, amit tudnod kell. A számításhoz a származékok hajtjuk kisegítő sor számítások (4. ábra).