Érdekelt a történelem, a Pitagorasz-tétel
és
Vannak úgynevezett pitagoreusi Tree - egy hipotetikus fa, amely áll egymással derékszögű háromszög, amelynek szára és épül az átfogó négyzetek.
A Pitagorasz-tétel következménye egy tetszőleges háromszög:
oldalán a háromszög egyenlő a négyzetgyökét négyzetének összege a másik két oldala mínusz kétszer a termék az oldalán a koszinusza a köztük lévő szög.
Egy vegyület Ez van írva, mint:
2 = b 2 + c 2 - 2BC * cos α
Ezt a vizsgálatot az úgynevezett koszinusztétel, de valójában - a Pitagorasz-tétel egy tetszőleges háromszög.
Három készítmények a Pitagorasz-tétel:
1. Egy derékszögű háromszög, a tér a átfogója egyenlő a négyzetének összege a másik két oldala.
2. A terület a tér épül átfogó egy derékszögű háromszög egyenlő az területének összege a négyzetek épül Catete.
3. A tér épül átfogó egy derékszögű háromszög, négyzet equidecomposable épül Catete.
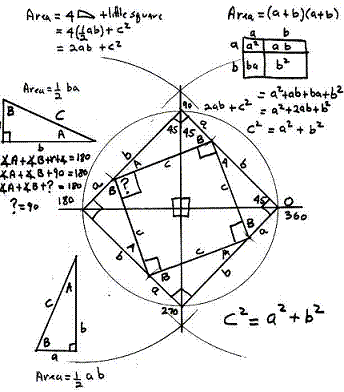
Az ábrán a két egyenlő négyzetek. A hossza minden oldalán egy négyzet egyenlő a + b. Mind a négyzetek részekre van osztva, amely a terek és derékszögű háromszögek. Nyilvánvaló, hogy ha a tér nagysága vegye négyszeres terület derékszögű háromszög lábakkal a, b, marad egyenlő területeket, azaz. E. C2 = a2 + b2. Azonban az ősi hinduk, aki nem tartozik ez az érv, általában nem írja meg, és a mellékelt rajz csak egy szót: „Nézd!” Lehetséges, hogy ugyanaz a felajánlott bizonyítékok és Püthagorasz.
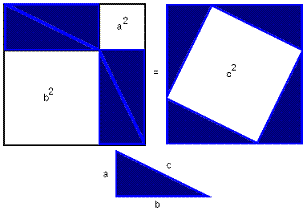
2) annak igazolását, Al-Nayrizi *
Proof Al-Nayrizi is nagyon egyszerű. Érdemes megjegyezni, hogy az összes darab megegyeznek egyenlő őket kizárólag párhuzamos fordítást.
D
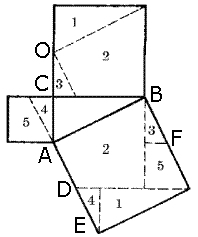
bizonyíték:
A rajz alapján világosan látható, hogy figruy. jelölt azonos szám egyenlő. A háromszögek 1, 1, 3, 3, 4, és a 4 egyenlő. Négyszögek 2, 2, 5 és 5 is megegyezik. Ennélfogva, a tétel bizonyított.
* - latinos neve - Annaritsy.
3) egyik lehetséges bizonyítási Püthagorász
Közül a bizonyítékokat a Pitagorasz-tétel algebrai módszer első helyen (talán a legrégebbi) kerül egy igazolást a hasonlóság. Itt egy modern előadás egyik ilyen bizonyíték, talán tartozó Püthagorasz.
Adott: ΔAVS - téglalap alakú, derékszögű C; CM - magassága; b1 - a vetítés a átfogója láb b, a1 - vetítés a láb és a átfogója.
Bizonyítás: Abból, amit ΔABC hasonló ΔACM alábbiak szerint:
A tény, hogy hasonló ΔABC ΔBCM alábbiak szerint:
Összecsukható távon távú egyenlet (1) és (2), megkapjuk a 2 + b 2 = CB1 + CA1 = C (b1 + A1) = C 2 .Teorema bizonyult.
Ha Pitagorasz igazán kínálnak ilyen igazolást, ő ismeri a számos fontos geometriai tételek, amelyeket a modern történészek matematika szokás tulajdonítani Euclid.
3) A bizonyíték Garfield
Adott: A közvetlen Három derékszögű háromszög.
Bizonyítás: Az ábrán három derékszögű háromszögek hogy egy trapéz. Ezért ezen a területen a szám megtalálható a következő képlet segítségével terület négyszögletes trapéz, vagy mint egy területének összege a három háromszög. Az első esetben, ez a terület
és a második esetben
ab / 2 + ab / 2 + c 2/2.
Egyenlővé ezeket a kifejezéseket, megkapjuk a tétel a Pitagorasz.
4) A bizonyítás alapul az elmélet a hasonlóság.
Egy derékszögű háromszög ABC tart a tetején a derékszög CD magassága; akkor a háromszög két háromszögre törik, amelyek szintén téglalap alakú. Az így kapott háromszög hasonló egymáshoz, és az eredeti háromszög. Ez könnyen bizonyítható segítségével az első jele hasonlósága háromszögek (két sarkok). Sőt, láthatjuk, hogy túl a derékszög háromszög ABC és ACD közös szög, a háromszögek ABC és a CBD - teljes szög b. Az a tény, hogy a kis háromszögek is hasonlóak egymáshoz, abból a tényből következik, hogy mindegyik olyan, mint egy nagy háromszög. Azonban lehet telepíteni közvetlenül.
mert Az Egy derékszögű háromszög mértani közepe közötti átfogó és a vetülete a lábát az átfogó, van:
Hozzáadja ezeket egyenletek Terminusonként kapjuk:
A tétel bizonyított újra.
Nicola Léonard Sadie Carnot (1824)