Előadás a gyémánt és szögletes
2 Diamond A gyémánt eltér paralelogramma? rombusz paralelogramma
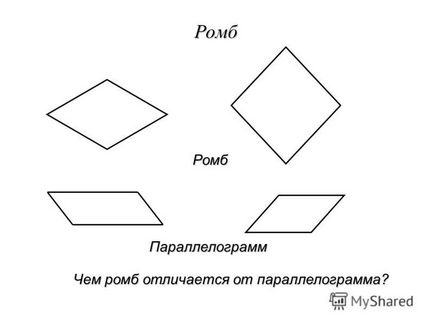
3 Diamond Definíció: Rombach úgynevezett paralelogramma amelynek minden oldala egyenlő. Mivel a gyémánt egy paralelogramma, akkor az összes tulajdonságait a paralelogramma A B C D O, milyen tulajdonságokat rombusz ABCD? 1) BO = OD, AO = OC 2) Gondolod, nincs több ingatlan a rombusz?
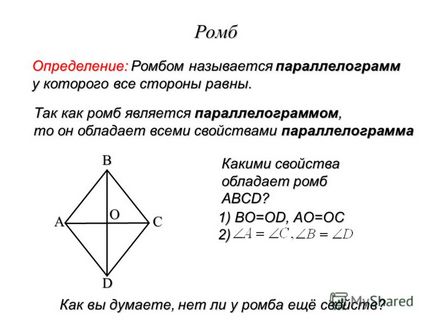
4 Property rombusz tulajdon: átlói rombusz merőlegesek, és ossza félbe sarkokban. Bizonyítás 1. AB = AD (definíció szerint rombusz) Adott: ABCD - rombusz ABCD ODokazat: AO = OC (paralelogramma tulajdonság) 4. Következésképpen AO - medián 5. A (2) és (4) az következik, hogy AO - magassága és felezővonal 6 . Ezért
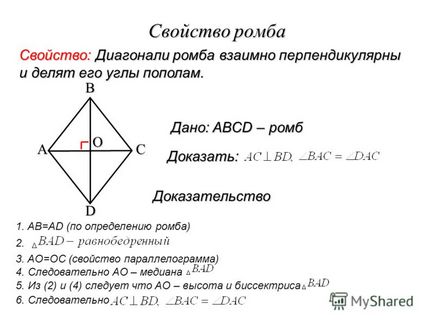
5. tér A tér eltér a téglalap? négyzet téglalap
6. tér Definíció: A négyzet hívják négyszöget, amelyben minden fél egyenlő. Egy téglalap paralelogramma, így a tér egy paralelogramma amelynek minden oldala egyenlő, azaz, egy rombusz. A tér minden ingatlan egy téglalap és rombusz.

7 Alap Tulajdonságok 1. Minden sarkában egy négyzet egy négyzet vonalak A BC D 2. átlói a tér egyenlő, kölcsönösen merőleges felezik metszéspont és felezik a szögek egy négyzet A BC D O
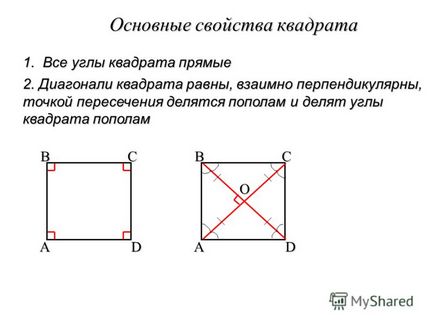
8 probléma megoldása Bizonyítsuk be, hogy a gyémánt, az egyik a szögek, amelyek a vonal téren. A BC D Igazoljuk: ABCD - négyzet Igazoljuk: ABCD - négyzet Adott: ABCD - rombusz bizonyítási 1.ABCD - rombusz által állapotban, tehát, AB = BC = CD = AD, 2. a hipotézis, így következésképpen 5. Minden oldal egyenlő és az összes szögek egyenlő, ezért az ABCD - négyzet
