Mode és a medián véletlen változók
Akkor vesz mod 2 értékek: d (X) = 3, és d (X) = 5.
Legyen X - folytonos valószínűségi változó sűrűségfüggvénye f (x). Divat ebben rv Ez az úgynevezett maximális pontját a valószínűség-sűrűség. Ez a maximális pont az f függvény (x) a hagyományos eljárással állíthatjuk elő a származék.
Példa. Mivel a valószínűsége sűrűsége IRV
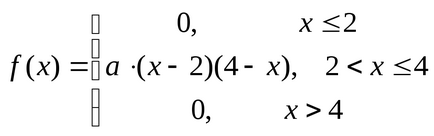
Keresse meg a értékét és a divat ez a véletlen változó.
Legyen X - folytonos valószínűségi változók. medián SV X (jelöli h (X)) nevezzük h szám. amely elosztja a száma vonal 2 időközönként (-∞, h) és a [H, + ∞). ahol DW X esik azonos valószínűséggel. Így, ha a medián h (X) = H, a következő egyenlőség
P (X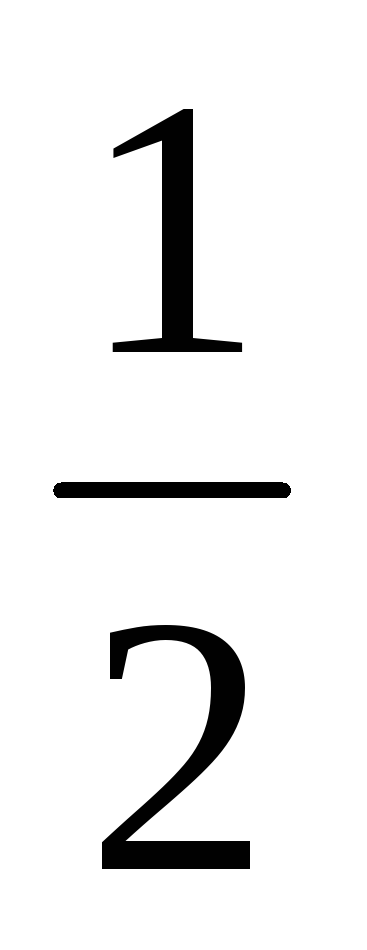
Megjegyezni, hogy a valószínűsége, P (X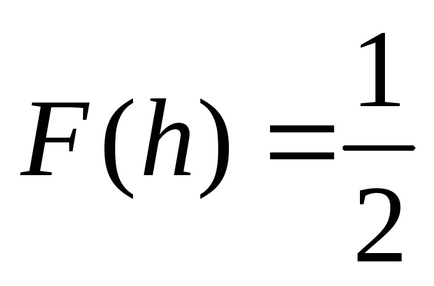
Ha a IRV megadott nem függvény F (x) eloszlás. és a valószínűsége sűrűsége f (x). emlékeztetve a kifejezés az elosztó funkció szempontjából a valószínűsége sűrűsége
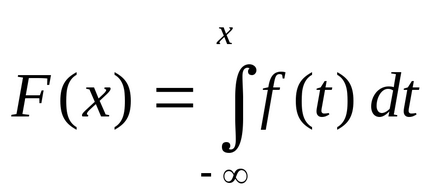
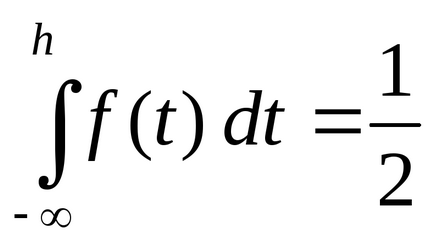
Medián h (X) folyamatos d.s. X keresi az egyik egyenletek írásbeli fenti (attól függően, hogy mi van megadva: F (x) vagy f (x)). Diszkrét valószínűségi változók medián nincs definiálva.
Példa. Keresse meg a medián IRV H. tekintettel annak eloszlásfüggvény
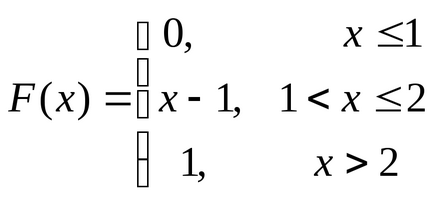
Néhány fontos jogszabályok eloszlása véletlen változók
A különböző eloszlás valószínűségi változók, néhány törvényi megtalálható a legtöbb alkalmazás. Ezért azok kapott általános képletű kiszámításához numerikus jellemzői: elvárás, diszperzió, mód, a medián és mások. Úgy ezeket a törvényeket forgalmazás.
binomiális eloszlás
Törvények közé eloszlása diszkrét valószínűségi változók a leggyakoribb a binomiális eloszlású, amely már felmerült tekintve az úgynevezett Bernoulli (az előfordulások számát az esemény egy sor független kísérletek).
Egy diszkrét X valószínűségi változó szerint vannak elosztva a binomiális törvény. ha értéke 0, 1, 2.n valószínűséggel p0, p1. pn. számítják az alábbi képlet szerint
,
ha az elosztórendszer p paraméter zárt nulla és egy közötti 0 ≤ p ≤ 1 és q = 1-p. Így H. d.s.v által forgalmazott binomiális jog, a törvény a következő eloszlásban:
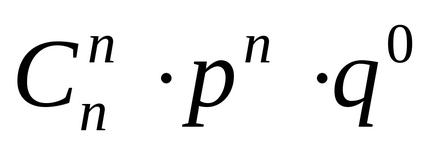
Mint már említettük, szerint a binomiális hatályos törvény értelmében a sikerek számát a Bernoulli rendszer. Legyen n független végzett vizsgálatok, amelyek mindegyikében egy esemény előállítása történhet ugyanazzal a p valószínűséggel. Tekintsük a rv X - az előfordulások számát az A minden n vizsgálatokban (azaz, a sikerek számát hívták korábban). Aztán dm X megfelelően oszlik meg a binomiális törvény. Azt találtuk a képlet a várakozást ezen véletlen változó, amelyek a képletek a matematikai várható értéke és szórása egy tetszőleges valószínűségi változó megfelelően oszlanak a Bernoulli-rendszer:
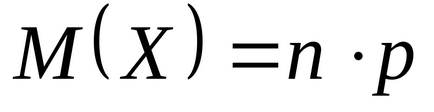
Találunk divat d (X) binomiális eloszlású X azaz A legvalószínűbb sikerek számát a Bernoulli rendszer. A definíció szerint a divat d (X) = k. ha a valószínűsége, hogy a legmagasabb az összes valószínűségek P0, P1. pn. Találunk egy k számot (ez egy pozitív egész szám). Ezzel a valószínűsége pk k nem lehet kevesebb a szomszédos valószínűségeket: pk-1≤pk≤pk + 1. Behelyettesítve helyett minden megfelelő képlet valószínűleg úgy találják, hogy a k szám meg kell felelnie a kettős egyenlőtlenséget:
.
Ha a festék képletek a kombinációk száma, és végezzen egyszerű átalakulás lehet szerezni, hogy a bal oldali egyenlőtlenség adja k≤ (n + 1) ∙ p. és a megfelelő k≥ (n + 1) ∙ p-1. Így a száma k megfelelnek a kettős egyenlőtlenséget (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. azaz tartozik az intervallum [(n + 1) ∙ p-1, (n + 1) ∙ p]. Mivel a hossza ezen intervallum nyilvánvalóan egyenlő 1, hogy lehet kapni egy vagy két egész szám. Ha a szám (n + 1) ∙ p egész szám, akkor az intervallum [(n + 1) ∙ p-1, (n + 1) ∙ p] 2-nek egész számok feküdt a végpontokban. Ha a szám (n + 1) ∙ p értéke nem egész szám, ebben az intervallumban csak egy egész szám.
Így, ha a szám (n + 1) ∙ p egész szám, a divat binomiális eloszlású valószínűségi változó X vesz két szomszédos értékeket. d (X) = (n + 1) ∙ p-1 és d (X) = (n + 1) ∙ p. Ha a szám (n + 1) ∙ p értéke nem egész szám, a divat binomiális eloszlású valószínűségi változó X egy értéke d (X) = k. ahol k az egyedi egész szám, kielégíti az egyenlőtlenséget (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. Ha az egyik emlékeztet arra, hogy a felvétel [a] azt jelenti, hogy egész részét a számot a. Ebben az esetben lehet írva d (X) = [(n + 1) ∙ p].
Példa. Cube feldobunk 100-szor. Mi a legvalószínűbb hatos csapadék?
Példa. Annak a valószínűsége, ütő a cél lövő 0.7. Keresse meg a legvalószínűbb száma a célt 30 lövés.
Példa. Valószínűsége termelés a hibás alkatrészek a gép egyenlő 0,06. Mi a legvalószínűbb hibás alkatrészek egy batch 200 rész, megmunkált ezen a gépen?
Példa. 7 bank kiadott hitelek. Köztudott, hogy nem tér vissza a kölcsönt átlagosan 2 kivéve 10. Keresse meg az átlagos száma a rossz hitelek.