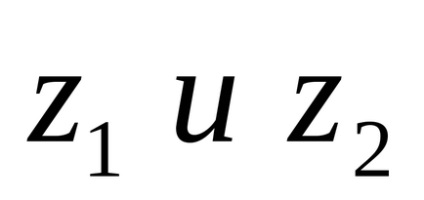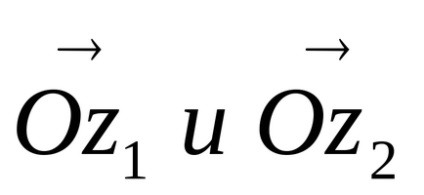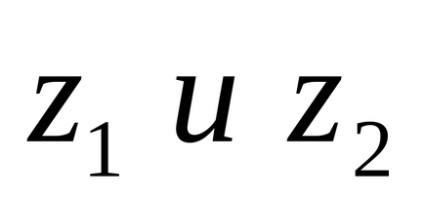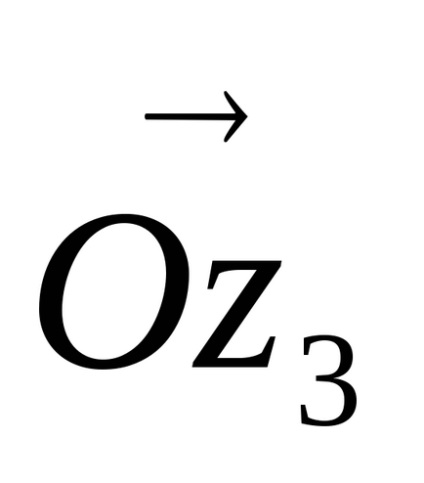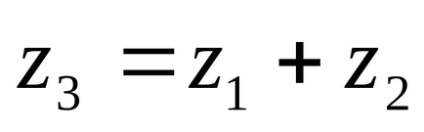Meghatározása komplex szám
Chislomz komplex úgynevezett szimbólum x + yi, ahol x és y - valós szám. Ahol x jelentése a valós része egy komplex szám, y - képzetes része, i - imaginárius egység.
A valós része a komplex szám jelöli Réz (Réz = x), és a képzetes rész jelöljük IMZ (lmz = y). Ezért egy komplex szám felírható.
Felvétel egy komplex szám
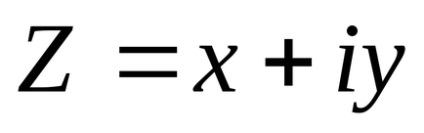
komplex szám
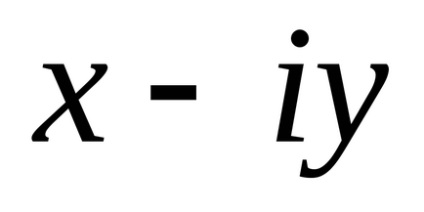
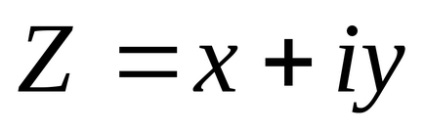
komplex számok
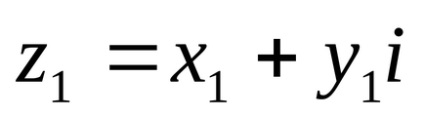
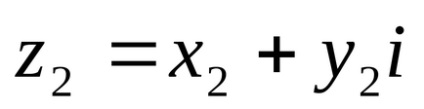
Ha y = 0, a komplex szám az űrlap
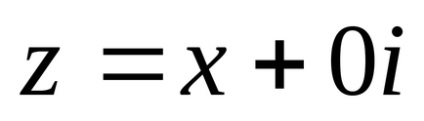
Ha x = 0, y ≠ 0, a komplex szám formában van z = 0 + yi vagy rövidebb, z = yi. Ez az úgynevezett képzetes számot. Különösen, ha x = 0, y = 1, megkapjuk a komplex szám
0 + 1i = i - imaginárius egység. Bármennyi z = x + yi, ahol y ≠ 0 nevezzük egy képzeletbeli számot.
Két komplex szám x + yi az x-yi - úgynevezett komplex konjugátum. Ha z = x + yi, a konjugátum a X-yi - általában jelöljük
Műveletek komplex számok.
Az összeget a komplex számok nevezzük komplex szám jelöli az
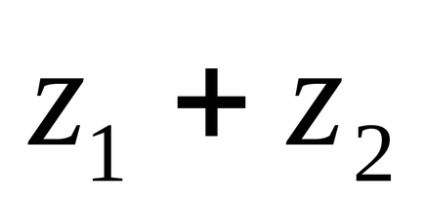
Ha hozzá komplex számok állnak valós és képzetes része.
komplex szám
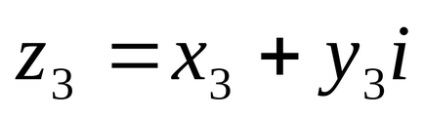
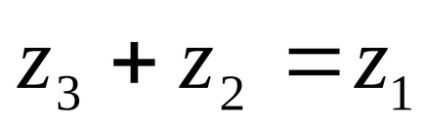
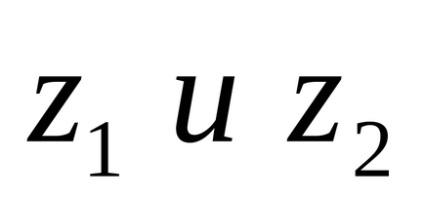
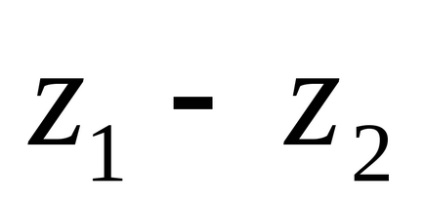
A meghatározás azt jelenti, hogy
Ha kivonva a valós és képzetes része a kisebbítendő kivonjuk illetőleg a valós és képzetes része a kivonandó.
A szorzás két komplex szám által bevezetett egyenlet
(4) egyenlet következik
Ha a szorzás a két komplex szám
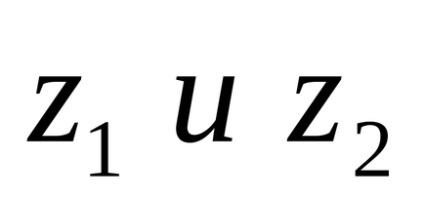
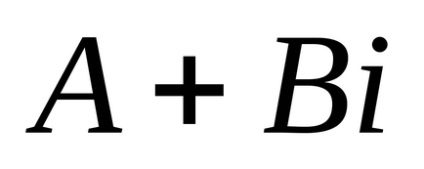
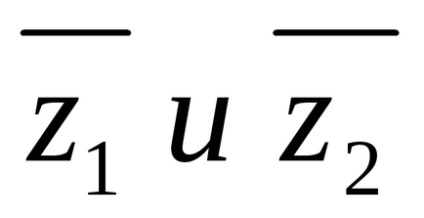
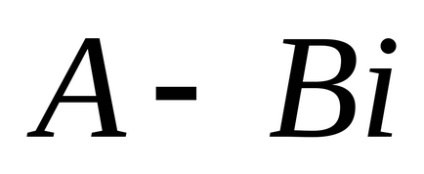
Az osztály kerül bevezetésre az inverz szorzás. A hányadosa száma hívószám
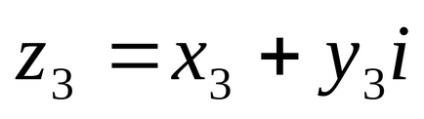
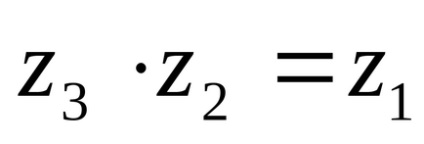
Ezért alapján (4), megkapjuk:
Megoldása a rendszer (7) képest
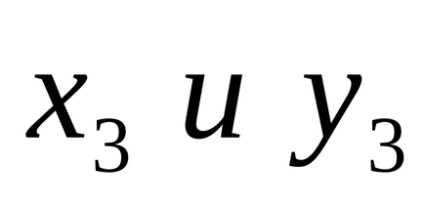
(ahol
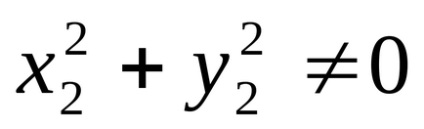
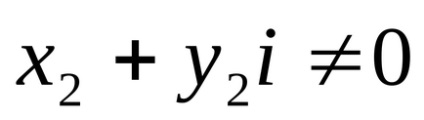
Könnyen belátható, hogy a (9) egyenletből lehet kiszámítani, hogy megszorozzuk a számláló és a nevező a frakció
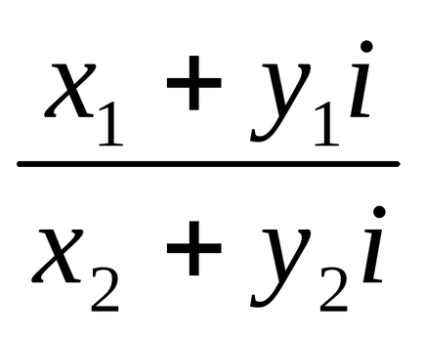
Az építőiparban a komplex szám Z n egy természetes teljesítmény tekinthető egy speciális esete a szorzás a komplex számok:
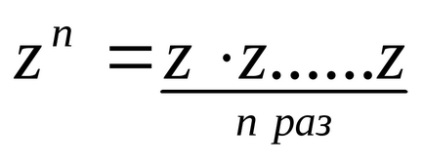
Komplex számok lehet tekinteni, mint egy kiterjesztése a valós számok halmaza. Tény, hogy az algebrai műveletek komplex számokkal lépett, így a összessége a „valóság” a komplex számok (azaz. E. számok az űrlap
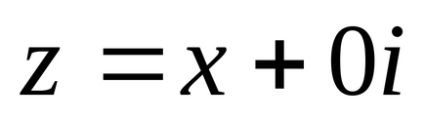
z = x a megadott műveleteket rájuk egybeesik a valós számok halmaza és az ismert intézkedések ezeket a számokat.
Trigonometrikus forma egy komplex szám. Mi választjuk ki a gépet XOY polár koordinátarendszerben (1.), Hogy a pólus egybeesett a származás, és a sarki tengely menne együtt a pozitív irányba a valós tengely. Jelöljük a polársugara pontok
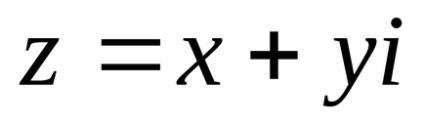
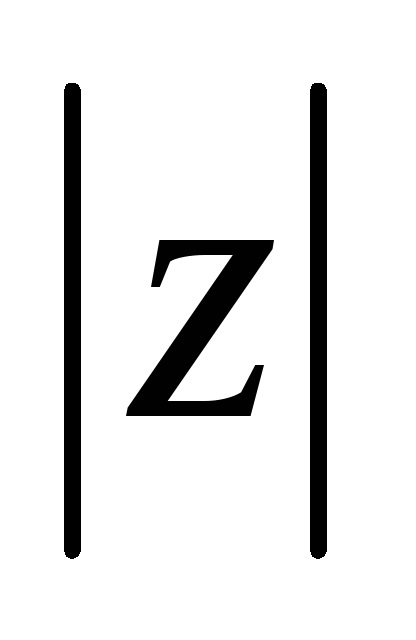
,
ahol k - tetszőleges egész szám, és φ - értékek bármelyikében az érvelés z. Mivel, amint
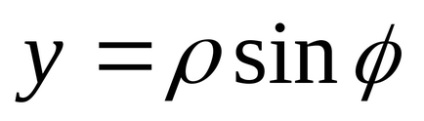
(*)
Az expressziós (*) a trigonometrikus formája egy komplex szám. Nyilvánvaló, hogy
A geometriai értelmezése a komplex számok összeadása. Hagyja, hogy a komplex síkon adott két szám
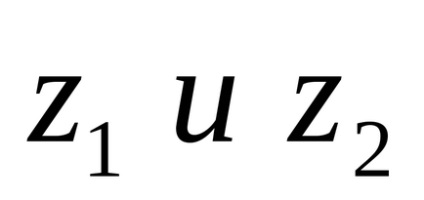
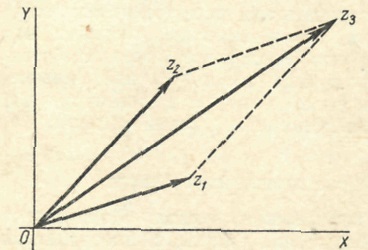
Sugarú vektorok pontok