Hogyan kell felhívni a háromoldalú piramis, - hogyan kell felhívni a háromoldalú piramis,

Rajz - az első és nagyon fontos lépés a megoldása geometriai probléma. Mi legyen a helyes alak a piramis?

Először Idézzük tulajdonságainak egyidejű mérnöki.

- párhuzamos vonalszakaszok ábrázolt figura párhuzamos szegmensek;

- az arány szegmensek hossza tárolt párhuzamos vonalak és vonalszakaszok kollineáris.

Ábra szabályos háromoldalú piramis

Első ábrázol bázis. Mivel a tervezés szögek és párhuzamos kapcsolat a szegmensek hossza nem párhuzamosak nem tárolja a bázis szabályos háromszög piramis ábrázolt tetszőleges háromszög.

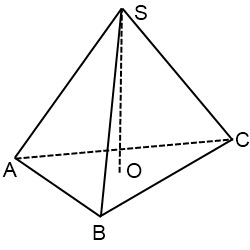
Center egy egyenlő oldalú háromszög - a metszéspontja felező a háromszög. Mivel a medián a metszéspont vannak osztva arány 2: 1, számított a felső, alapcsúcs mentálisan össze a közepén a szemközti oldalon, kb osszuk három részből áll, és a két rész a régióban a vertex munkapont. Ettől a ponttól felfelé a merőleges. Ez - a magassága a piramis. Merőleges készít olyan hosszú, mint az oldalsó széle nem zárta magasság képet.

Ábra rendszeres négyszögletes piramis

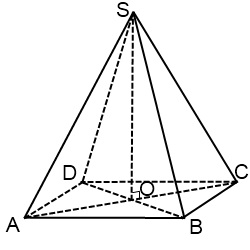
Ábra rendszeres négyszögletes gúla is kezdve a bázis. Mivel a párhuzamos szegmensek menti, és a szögek - nincs, a tér alján a paralelogramma van ábrázolva. Kívánatos, hogy a hegyesszög a paralelogramma do kisebb, míg az oldalfelületek kapunk többé. A tér közepén - a metszéspontja az átlók. Tartjuk átlósan metszéspontja merőleges visszaállítani. Ez merőleges - a magassága a piramis. Kiválasztása a merőleges hossza úgy, hogy az oldalsó bordák nem olvasztott össze.

Ábra szabályos hatszög piramis

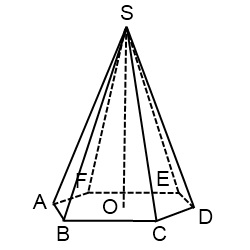
Mivel a párhuzamos tervezési párhuzamos vonalszakaszok van tárolva, a bázis szabályos hatszög piramis - egy szabályos hatszög - ábrázolják egy hatszög, amelyekhez az egymással ellentétes oldalai párhuzamosak és egyenlő. Közepén egy szabályos hatszög - a metszéspontja az átlók. Annak érdekében, hogy ne feleslegesen a rajz, átlós nem rendelkezik, és kiderül, hogy pont szól. Visszaállítása merőleges abból - a magassága a piramis - úgy, hogy az oldalsó élek nem olvasztott össze.

Megszerkesztésében „aranymetszés” figyelmét elsődleges értéke 7, 23 cm. Továbbá, az együttható számolni „aranymetszés”. Ez a szám a különböző tudományok és egyenlő 1.618. Szorzás 72,3 mm 1618, kapsz 116,981 mm. Az érték lehet kerekíteni - 117 mm-es, ez lesz egyenlő a bázis oldalán a piramis. Így - 7.2 cm - magassága a piramis, 11,7 cm-es - oldalán az alap a piramis.

Most számít a méret a háromszög arcok, a „törvény Püthagorasz” kapsz 92,769 cm kerekítse az érték 9,3 cm. Vegyünk egy ceruza, vonalzó és a papír, rajzoljon négy háromszög paraméterekkel 11,7 * 9,3. Ha a piramis alapja, hogy szükség van még egy négyzet oldala 11,7 * 11,7 * 11,7 * 11,7. Kötvény oldalán a piramis ne használjon csavarokat szegek és csavarok - energia a piramis lesz törve.

Rendezzük háromszögek oly módon, hogy kapjunk egy piramis, elindította a széles oldalon a táblázatot. Biztonságos háromszögek szélén szalag, ragasztószalag, vagy rögzítse papírra ragasztva szegmensek.

Igazítsa az első és a negyedik arc szögek pont a lehető legpontosabban. Forduljon. zárjuk le a belső varratok. Ellenőrizze a méret a négyzet alapú. Tedd ragasztott háromszögek, hagyja, hogy a ragasztó biztosított.

A kapott modellje a piramis üreges. Ha ez elég, akkor hagyja el a piramis ebben a formában - ha nem, ragaszkodni az alapja a kupola. Cél a forrás pozitív energiát az egyes problémák megoldásához.

Állítsa be a programot a konkrét információk. A festék a piramis a kedvenc színe, illeszteni a képet készít mintát, írj kívánságait. Használd, mint egy energiaforrás, megjelölve rajta arcok fotóit. Töltsük fel a tartályt vízzel, fedjük le egy kupola piramis. A víz meg fog változni a tulajdonságait, és vált az „élő”.

Self-hipnózis, vagy sem, a lényeg - bizalom az információt, és a jó gondolatok valóra szükséges.

Piramis (πυραμίς πυραμίδος.) -. amelyek közül az egyik felülete (úgynevezett okok) - tetszőleges. és a másik oldal (az úgynevezett oldalsó élek) -. egy közös csúcsa. Mivel a szögek száma a bázis háromszög piramis megkülönböztetni (), négyszögletes, stb A piramis egy különleges eset.

A történelem a fejlődés a piramis geometria

Kezdés geometria piramis kezdett az ókori egyiptomi és babiloni, de aktívan fejlesztett az ókori Görögországban. A kötet a piramis ismert volt az ókori egyiptomiak. Az első görög matematikus, aki létrehozta, mi a térfogata a gúla volt. és bebizonyította. Görög matematikus rendszerezett tudás a piramis a XII volumenét. és első meghatározás vezetett piramis: testi ábra által határolt síkok, hogy egy síkban konvergálnak egyetlen pontban (a könyv XI, definíció 12).

elemei a piramis

SO - magassága
SF - apothem
OF - a sugara a beírt kör a tövénél

• - a magassága a jobb oldallapjának a piramis lefolytatott annak csúcsait;
• oldalfalakon - háromszögek konvergáló a csúcsnál;
• oldalirányú bordák - közös oldalán oldalfelületek;
• tetején a piramis - pont, összekötő oldalsó élek és fekvő bázis síkban;
• magassága - a merőleges szegmens átszívott a piramis vertex, hogy az alap síkjában (a végei ebben a szegmensben a piramis csúcspont és a felületi normális);
• átlós részének a piramis - piramis-szakasz átmegy a felső és az alap az átló;
• bázis - poligon, amely nem tartozik a piramis csúcsára.

piramisok söprés

A Sweep ötszögű piramis:
1. A sík az alap ( „csillag”)
2. síkjában egyik oldalsó felületek

Ez az úgynevezett sweep-síkidom kombinálásával kapott a mértani felület a test egy sík (anélkül metszettel vagy más felületi elemek egymáshoz). Ismerkedés a tanulmány a szkennelés felszíni, az utóbbit kell tekinteni, mint egy rugalmas, nem nyújtható film. Néhány felületek így hajlító össze a gépet. Ebben az esetben, ha a felület a rekesz kombinálni lehet egy síkban szakadás nélkül, és ragasztás, a felület egy ilyen hívás fejleszthető, és a kapott sík alakja - a sweep.

A tulajdonságok a piramis

Ha minden oldalsó szélei egyenlő. akkor:

• alapja körül a piramis lehet leírni, mint egy kör, a tetején a piramis az előrejelzések a közepén;
• oldalsó szélei formában, a alapsíkon egyenlő szögek;
• Ennek a fordítottja is igaz, azaz ha az oldalélek alkotnak alapsíkkal egyenlő szögtávolságra, vagy ha közel az alján a piramis lehet leírni, mint egy kör, a tetején a piramis az előrejelzések a közepén is, minden oldalsó szélei a piramis egyenlő.

Ha az oldalsó felületek vannak döntve, hogy az alap sík ugyanolyan szögben. akkor:

• Az alapja a piramis, akkor helyezni egy kört, a tetején a piramis az előrejelzések a közepén;
• a magassága a oldalfelületek egyenlő;
• egy oldalfelülete felével egyenlő a termék a bázis az oldalsó szélén.

Tétel összekapcsolása piramis más geometriai testek

Leírás körének jobb a piramis köré:
SD - a magassága a piramis.
AD - kör sugara leíró bázis.
A - a középső borda oldallap
C - metszéspontja a síkok közepén áthaladó az élek merőleges őket.
AC = CS - gömb sugara leírja a piramis

Sphere írt szabályos piramis:
D - Base Központ
SF - apothem
ASD - felezővonal síkja közötti szög az oldalsó felületek
BCE - felezővonal síkja közötti szög a bázis és az oldalsó felület
C - a metszéspontja a felezővonal sík
CK = CD - a gömb sugarának feltüntetik egy piramis

• Meg lehet leírni kb piramis gömb, amikor az alapja a piramis egy sokszög, amely körül leírható egy kör (szükséges és elégséges feltétele). A gömb középpontja a metszéspont a síkok áthaladó felezőpontja a széle a piramis arra merőleges. E tételből, hogy bármely mintegy három- és bármilyen szabályos piramis leírható hatálya;
• a piramis lehet feliratos gömb, amikor a belső piramis találkozik egy ponton (). Ez a pont lesz a központja a gömb.

• Cone úgynevezett írt egy piramis, ha a csúcsok egybe és alapja van írva az alapja a piramis. És adja meg a piramis kúp csak ha apothem piramis egyenlő (a szükséges és elégséges feltétele);
• Cone úgynevezett piramis leírt, mikor azok csúcsok egybeesnek, és alapja van leírva a bázis közelében a piramis. Továbbá leírják egy kúp a piramis köré csak, ha az összes oldalélei a piramis egyenlő (a szükséges és elégséges feltétele);
• Magasság ilyen kúpok és gúlák egyenlő.

• A henger helyezhető be egy piramis nevű, ha annak egyik bázis egybeesik a beírható kör keresztmetszete a piramis egy sík párhuzamos az alapelem és a másik bázis tartozik az alapja a piramis.
• Henger, le körülbelül piramis, piramis csúcsa, ha tartozik egy bázis, és alapja van leírva a másik a bázis közelében a piramis. És írja le a hengert a piramis köré lehet csak az alján a piramis - a beírt sokszög (a szükséges és elégséges feltétel).

Formula társított piramis

• piramis lehet számítani a következő képlet:

. V = 1 március S h> Sh,> ahol S - a bázis és H - magassága; V = 1 június V o.> V_

,> Amennyiben V p> - parallelepipedon térfogata;

• Továbbá, a hangerőt a háromszög alakú piramis (Tetrahedron) lehet képlettel számítottuk ki:

. V = 1 június 1 2 d sin ⁡ φ> a_a_d \ sin \ varphi,> a, ahol a 1 2, a_> - ferde éleket. d - közötti távolság egy 1> 2, és a>. φ - közötti szög 1> 2, és a>;

• Az oldalsó felülete - az összege a területek az oldalfelületek:

S b = Σ i S i = \ sum _ ^<>S_>

• Gross felülete - az az összeg, terület az oldalsó felületének a bázis:

S p = S b + S o = S_ + S_>

• Ahhoz, hogy megtalálja a területet a palástfelület egy piramis a megfelelő képlet használható:

S b = 1 február P a = n 2 b 2 s i n α => Pa => b ^ sin \ alpha>, ahol egy -. P - bázis, n - a száma oldalán a bázis, b - oldaléle, α - sík csúcsszöge a piramis.

Különleges esetekben a piramis

rendszeres piramis

A piramis azt mondják, hogy a rendszeres, ha annak alapja. és a vertex az előrejelzések a közepén a bázis. Ezután a következő tulajdonságokkal rendelkezik:

• oldalsó szélei a piramis helyes;
• a jobb oldalon arcok a piramis összes - egyenlő szárú háromszögek;
• minden rendszeres piramis egyaránt levelet, és leírja a hatálya körülötte;
• ha a központok a beírt és körülírt gömbök az azonos, az összeg a sík szögek a tetején a piramis egyenlő tc. és mindegyik, illetve π n >>. ahol n - száma sokszögoid a bázis;
• jobb oldali felülete a piramis fele a termék egy bázis apofemu.

téglalap alakú piramis

Piramis úgynevezett négyszögletes, ha az egyik oldalsó szélei a piramis merőleges az alapra. Ebben az esetben ez a szélén és magassága a piramis.

Tetraéder hívják, egy háromoldalú piramis. Mindenesetre az arcok a tetraéder lehet venni, mint az alap a piramis. Ezenkívül van egy nagy különbség a „szabályos háromoldalú piramis” és „” Egy szabályos háromoldalú piramis - egy piramis egy egyenlő oldalú háromszöget alul (a szélét meg kell egyeznie egyenlő szárú háromszögek). Szabályos tetraéder egy tetraéder, amelynek minden arcok egyenlő oldalú háromszög.

jegyzetek

irodalom