Kiszámítása határozott integrál
> Quadrature képletek szerint számítjuk ki a (3) képlet, a megfelelő kvadratúra nevű képlet kvadratúra típusú interpolációs képlet.
> Quadrature képletű (2) egy előre meghatározott helyen a csomópontok
Nem függ a formáját az integrandus.
2. A típus kvadratúra képletek interpolációs fennmaradó Rn [f] lehet leírni, mint egy értéket adja differenciáloperátor f (x). mert
.
3. polinomok n-edrendű befogadó kvadratúra képletű (2) éles, azaz a
. A legmagasabb fokú polinom, amelyre pontos kvadratúra képlet, az úgynevezett fok kvadratúra- formula.
Tekintsük a konkrét esetben a (2) képletű és a (3): A módszer: téglalapok, trapézok, parabola (Simpson módszer). A nevek ezek a módszerek miatt geometriai értelmezése a megfelelő képletekkel.
Határozott integrál az f (x):
számszerűen egyenlő a terület a görbe trapéz által határolt görbék y = 0, x = a, X = b, y = f (x) (ábra. 1).
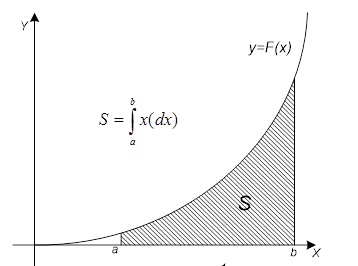
Ábra. 1 A görbe alatti terület y = f (x) kiszámítására a tér az egész integrációs [a, b] megosztjuk n egyenlő részintervallumokra hosszúságú h = (b-a) / N. A görbe alatti terület közelíteni integrandust helyébe a területének összege a téglalapok, ábrán látható (2).
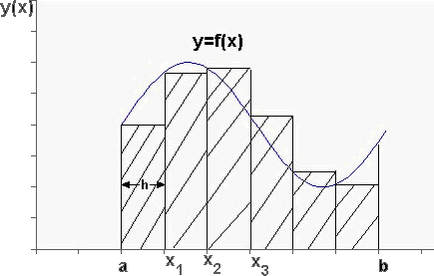
Ábra. 2 A görbe alatti terület y = f (x) közelítjük a területének összege a téglalapok
A területének összege az összes téglalapok számítják az alábbi képlet szerint
Módszer általános képletű (4) hívják a bal négyszög, és a módszer általános képletű (5) - a jobb téglalapok:
A hiba úgy határozzuk meg, hogy kiszámítjuk a szerves az integrációs lépésben h. Minél kisebb az integráció lépésben, annál pontosabb az integrál összeg S közelíti az integrál értéke I. alapján ennek az algoritmusnak van kialakítva, hogy kiszámítja az integrál egy előre meghatározott pontossággal. Úgy véljük, hogy az integrál összeg S a szerves értéke I C pontossággal eps, ha a különbség abszolút értéke közötti szerves összegek
, számított h lépés és a H / 2, illetve kevesebb, mint az EPS.
Módszer Közepes téglalap
Ahhoz, hogy megtalálja a határozott integrál szekunder téglalapok által határolt területen egyenes vonalak által a és b, feloszthatjuk n téglalapok azonos bázis H, a magasban a téglalapok a metszéspontok f (x) a felezőpontja az téglalapok (h / 2). Az integrál számszerűen egyenlő a területének összege a téglalapok n (3. ábra).
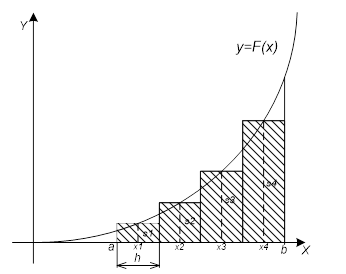
Ábra. 3 A görbe alatti terület y = f (x) közelítjük a területének összege a téglalapok
,
n - a partíciók számát a [a, b].
Ahhoz, hogy megtalálja a határozott integrál trapéz módszerrel íves trapéz területe is osztva n téglalap alakú trapéz bázisokkal h magassággal és y1. v2. v3. yn. ahol n - több négyszög trapéz. Az integrál számszerűen összegével egyenlő területek trapézok téglalap (4. ábra).
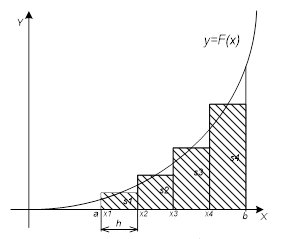
Ábra. 4. A görbe alatti terület y = f (x) közelítjük a területének összege a téglalap alakú trapéz.
N - partíciók számát
Pontosság trapéz szabály becsült száma
Pontosság trapéz szabály növekvő
gyorsabban csökken, mint a hibát használ téglalapok. Ennélfogva, a trapéz alakú képlet lehetővé teszi, hogy nagyobb pontossággal, mint a módszer téglalapok.
Ha minden egyes pár szegmensek
konstrukció a polinom a második fokozat, majd hogy integrálni a szegmens
és az adalékanyagot használni tulajdonsága az integrál, megkapjuk a képlet a Simpson.
A Simpson módszer, hogy kiszámítsa a határozott integrált egész integrációt [a, b] osztjuk al-időközönként egyenlő hosszúságú h = (b-a) / N. A szegmensek száma a partíció páros szám. Majd, mindegyik pár szomszédos részintervallumok integrandus függvény f (x) helyébe Lagrange polinom másodfokú (5. ábra).
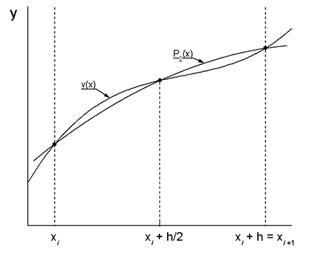
Ábra. 5 függvény y = f (x) intervallumban
helyébe a polinom 2. sorrendben
Tekintsük az integrandus
. Mi kicseréljük ezt integrandusz Lagrange interpolációs polinom másodfokú, amely egybeesik az y =
:
.:
Bemutatjuk a változás változók:
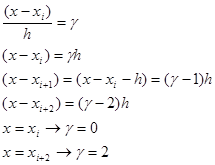
Figyelembe véve képletű helyettesítések,
Integrálása, megkapjuk a képlet a Simpson:
Kapott szerves
érték egybeesik területe ívelt trapéz határolt tengely
,
és a parabola pontokon átmenő
Simpson-féle képlet a következő lenne:
A képletben a parabola függvény értéke az f (x) a páratlan pont x1 partíció. x3. 2N-1-nek együtthatója 4, a még rámutat x2. x4. H2N-2 - 2 faktorral és két határpontok x0 = a, xn = b - 1 együttható.
A geometriai jelentését Simpson-féle képlet: alatti terület a grafikon görbe vonalú trapéz funkció f (x), az [a, b] helyébe a területek összege megközelítette számok alatt fekszik, parabola.
Ha az f (x) az [a, b] a negyedrendű folyamatos származék, az abszolút értéke hiba Simpson-féle képlet nem több, mint
ahol M - legnagyobb érték
a [a, b]. Mivel n 4 gyorsabban növekszik, mint a hiba n 2 Simpson formula n növelésével csökken lényegesen gyorsabb, mint a hiba trapéz szabály.
Ez integrál könnyen kiszámítható:
Vegyük n egyenlő 10, H = 0,1, a számított érték a integrandust
azokon a pontokon a partíció
, valamint a fél egységnyi helyeken
.
A képlet szerint másodlagos téglalapok kapjunk Ipryam = 0.785606 (hiba = a 0,027%), trapéz Itrap = 0,784981 (hiba körülbelül 0,054. Az eljárást alkalmazva a bal és a jobb téglalapok hiba több, mint 3%.
Pontosságának összehasonlítása közelítő képletek kiszámításához szerves újra
,
de most az alábbi képlet szerint Simpson, ha n = 4. Osszuk a [0, 1] négy egyenlő részre a pontok X0 = 0, x1 = 1/4, és x2 = 1/2, x3 = 3/4, x4 = 1, és kiszámítja a közelítő értéke az f (x) = 1 / ( 1 + x) ezeken a pontokon: y0 = 1,0000, 0,8000 y1 = y2 = 0,6667, = 0,5714 y3, y4 = 0,5000.
Szerint a Simpson-féle képlet megkapjuk
Úgy becsüljük, a hiba az eredmény. A integrandus függvény f (x) = 1 / (1 + x), van: f (4) (x) = 24 / (1 + x) 5. Ebből következik, hogy a [0, 1]
. Így tudjuk venni M = 24, és az eredmény a hiba nem haladja meg a 24 / (2880 × április 4.) = 0,0004. Összehasonlítva a közelítő érték egy pontos, arra a következtetésre jutunk, hogy az abszolút hiba a kapott eredményt az általános képletű Simpson kevésbé 0,00011. Ez összhangban van a fent megadott becslési hiba, sőt, azt jelzi, hogy lényegesen pontosabb Simpson formula trapéz szabály. Ezért a képlet a Simpson közelítő kiszámítása határozott integrálok használják gyakrabban, mint a trapéz szabály.
Összehasonlítása módszerek pontossági
Összehasonlítása módszerek pontossági erre a célra kiszámítjuk a beépített függvény az y = x, y = x + 2, y = x 2, ha n = 10 és n = 60, a = 0, b = 10. A pontos érték a integrálok rendre: 50, 70, 333. (3)
Az 1. táblázat azt mutatja, hogy a legpontosabb integrál talált Simpson-féle képlet kiszámítása során lineáris függvény az y = x, y = x + 2 megvalósítható úgy is, precíziós módszereit közegben téglalapok és trapézok, téglalapok jobb módszer kevésbé pontos. 1. táblázat azt mutatja, hogy számának növelésével a partíciók N (számának növekedése az integráció) pontosságát javítja a közelítő kiszámítása integrálok
A feladat laboratóriumi munka
1) Írja a program kiszámítja a határozott integrál módszer: középen, jobbra téglalap, trapéz és Simpson-féle módszerrel. Végezzük el az integráció a következő funkciókat tartalmazza:
a [0, 1] egy lépéssel
,
,
3. Run opciót egyéni feladatokat (2. táblázat)
2. táblázat Az egyes munka lehetőségek