A számossága a kontinuum - studopediya
Végtelen sok eleme, amelyet nem lehet számozni. Az ilyen halmazokat nevezzük megszámlálhatatlan.
Cantor-tétel. A készlet minden pont a szegmens [0, 1] megszámlálhatatlan.
Hagyja a beállított pontot a szegmens [0, 1] megszámlálható. Ezért, ezeket a pontokat lehet felsorolt, T. E. elhelyezkedő formájában x1 szekvenciát. x2 ... xn. ....
Osszuk a [0, 1] három egyenlő részre. Ahol a pont x1. ez nem tartozik minden szegmensben. . . Ezért néhány közülük D1 szegmens. nem tartalmazó pont x1 (ábra. 1.7). Vegyük ezt a darabot a D1 és osszuk három egyenlő részre. Közülük mindig van egy szegmense D2. amely nem tartalmazza a pont x2. Osztjuk az intervallumot három egyenlő részre, és így tovább. E. szerezzük szegmensek sorozatában D1 É D2 É D3 É...Édn É.... A Cantor axióma konvergál egy pont x n ® ¥. Szerkezetileg ez az x pont tartozik minden egyes szegmens D1. D2. D3, ..., Dn. ..., m. E. Lehet, hogy nem esik egybe bármelyike pontok x1. x2, ... xn. ..., T. E. A szekvenciája x1. x2 ... xn. ... nem terjed ki minden pont a [0, 1], ami ellentmond az eredeti feltételezést. Ez azt bizonyítja, a tétel.
Állítsa egyenértékű a készlet minden pont a szegmens [0, 1] beállítása folytonosság.
Mivel több időközönként pontok, vonalak és az egész vonalon azonos egymással, mindegyiknek lesz számossága a kontinuum.
Annak bizonyítására, hogy a halmaz egy számossága a kontinuum, elegendő, hogy jelezze egy-egy levelezés között ezt meg, és a beállított pontot a szegmensben, vagy az egész sort intervallumot.
Ábra. 1.8, hogy több pontot a parabola y = x 2 egyenértékű a beállított pontot a sor - ¥ 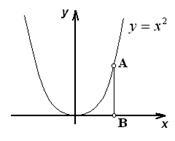
Állítsa be a számossága a kontinuum, akkor is használhatja az alábbi tétel a számossága a kontinuum-készletek (benyújtott bizonyítékok nélkül).
1. Tétel A mind részhalmazainak halmaza megszámlálható megszámlálható.
2. tétel A szett irracionális számok számossága van a kontinuum.
3. tétel A szett minden pont a n-dimenziós térben minden n van egy számossága a kontinuum.
4. Tétel A készlet minden komplex számok is számossága a kontinuum.
5. Tétel A szett folytonos függvények, az [a. b] egy számossága a kontinuum.
Így a hálózati végtelen halmazok változhat. A hatalom a kontinuum nagyobb, mint a hatalom egy megszámlálható halmaz. A válasz arra a kérdésre, hogy van-e több nagyobb teljesítményű, mint a hatalom a folytonosság, az alábbi tétel (adott bizonyítás nélkül).
Tétel a nagyobb teljesítmény készletek. A készlet minden részhalmaza egy adott halmaz nagyobb a kapacitása, mint az adott készlet.
Ebből következik, hogy a tétel készleteknek a lehető legnagyobb teljesítményt nem létezik.
TÁRGY 2. kapcsolatok. JELLEMZŐI