Faelemek 1
meghatározás
Faelemek - adatstruktúrát, amely lehetővé teszi, hogy végre műveleteket számos szegmensében a tömb $ O (\ log N) $. Fa darab - egy univerzális adatszerkezetet, amely lehet megvalósítani korlátlan műveletek sorozata (néha rendkívül összetett: $ O (\ log ^ 2 N) $). A legegyszerűbb változat a hossza a fa segítségével megtalálhatja az összeg vagy a minimális időköz, és módosíthatja az egyes elemek.
Építőipari szakaszok fából
Faelemek - teljes bináris fa, amelynek minden csúcsa felelős egy szegmense a tömbben. A gyökér a fa felelős a teljes tömb, két kiegészítő csúcsok - két részre, és így tovább. Minden csomópont felelős a részén nagyobb hosszúságú $ 1 $, két leányvállalata csúcsokat, amelyek a bal és jobb félre ezen intervallum. levelek a fa szegmensek felelősek az egyes elemek (hosszúságú szegmenst $ 1 $).
Grafikusan, ez a következő (az egy sor 8 elemek):
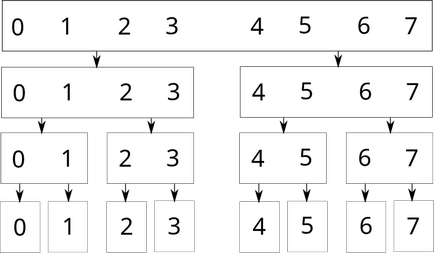
Minden doboz - felső szegmensében a fa. Ha néhány csúcs felel hossza páratlan hosszúságú, akkor annak egyik gyermek csomópontok feladata lesz a szegmens hossza $ \ lceil \ rceil $, és a többi - az a szegmens hosszát $ \ lfloor \ rfloor $. Például, így néz ki, mint egy fa szegmens számára egy sor 13 elemek:

A tömb $ n $ elemek faelemek körülbelül $ 2n $ csúcsainak ($ n + + + \ ldots $), és a magassága a sorrendben $ \ log n $.
A fő szegmense a fa tulajdonság, amelyre épülnek mind az algoritmusok dolgoznak vele a folyamatos szegmens tömb $ n $ elemeket is képviseli a $ 2 \ log n $ csúcsot a fában szegmensben.
Például, a szegmens $ [1; 11] $ array hossza $ 13 $ lehet, amelyet a következő csúcsok:
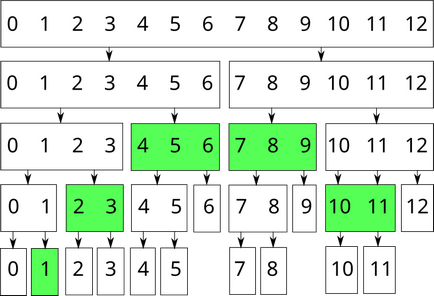
Faelemek megtalálni az összeg
Az egyik legegyszerűbb funkciók, amelyeket fel kell venni a $ O (\ log N) $ segítségével fadarabok - az összeget.
Az építőiparban a fa minden egyes felső fogja az összeget a megfelelő időtartam (az építési kerül sor rekurzív, így egyszerűen összeadja az összeg két szegmense leányvállalata). Ezután minden kérés összeget a szegmens lesz felosztva 2 $ \ log n $ szegmenseket, és megtalálják a mennyisége egyenként őket $ O (1) $ segítségével predproschitannye értéket. Így a komplexitás a kérelem összege $ O (\ log N) $.
Amellett, hogy az összeget a kéréseket a faelemek is csinálni kérelmek módosítására az egyes elemek (módosítás). Megjegyezzük, hogy a változó egyik eleme az összeg változni fog a felső egy minden szinten a fa szegmensek (amely tartalmazza ezt az elemet). Korrigált érték (ismét rekurzívan) csak ezen csúcsok. Így módosítási kérelmet bonyolultsága megegyezik a fa magasságát, vagy $ O (\ log N) $.
Végrehajtani a kérést, és az összeg módosítását a lekérdezésnek fa bejárás hajtja végre ugyanazt az algoritmust alapján DFS. Hagyja, hogy a határait kérésünket $ [L; R] $ (esetén módosítási kérelem $ L = R $), és a szegmens határánál megfelelő a jelenlegi csúcs $ [TL; TR] $. Attól függően, hogy a relatív pozíciója ezeket a határokat, három lehetőség van algoritmus:
A jelenlegi szegmens teljes mértékben tartalmazza a lekérdezés ($ L \ le TL; TR \ le R $).
Ha a kérelem az összeg predproschitannuyu visszatérítés összegét a szegmensben. Ha ez a módosítási kérelmet, és módosíthatja az elem újraszámítása összeg. A gyermek csomópontok nincs szükség, hogy menjen le.
Az aktuális szegmens nem teljes egészében szerepel a kérés ($ TR Nincs szükség beavatkozásra, egyszerűen hagyja a funkciót. Ha a kérelem az az összeg visszatérítésére $ 0 $. Jelenlegi szegmens részben szerepel a kérésben. Hívja a függvény rekurzívan a két lánya szegmensben. Ha ez az összeg a kérelem, visszatéríti az összeget a két kapott értékek. Ha ez a módosítási kérelem, újratervezi az érték összege az aktuális szegmens (mivel lehet, hogy megváltozott). Jelöljük ezeket a lehetőségeket, illetve zöld, piros és sárga. Akkor az összeg a kérelem a szegmens $ [1; 11] $ array hossza $ 13 $ kerül feldolgozásra az alábbiak szerint: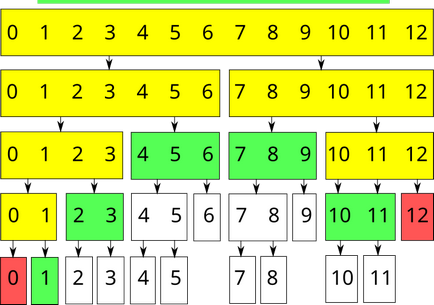
A módosítási kérelem $ 4 $ edik eleme:
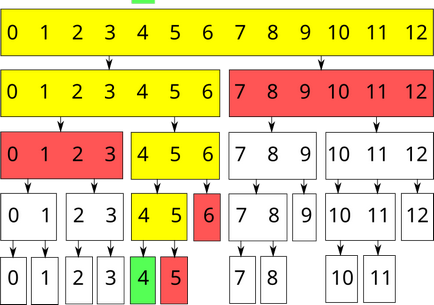
Megvalósítása a fahosszúságnyira megtalálni az összeg
Komplett bináris fa jelen, amint az előadást a halom, és egy sor képletek átmenet $ l = 2V $ és $ r = 2v + 1 $. Annak megakadályozása érdekében minden lehetséges túlfolyó méretű fadarabot a tömb $ n $ elemeket meg kell egyeznie $ 4n $.
Végrehajtás C ++:
Megvalósítása a fa magasságának keresni egy minimális
Ahhoz, hogy megtalálja a minimális kell változtatni a korábbi végrehajtása csak néhány sort:
Fák szegmensek, megőrizve az összes elemet
Megoldani bizonyos problémákat a csúcs, amely felelős a szegmens, meg kell tartani az összes elemet ebben a szegmensben a sorrend. Úgy tűnhet, hogy ez hogy túl sok memóriát, de ez nem az. A tömb mindegyik eleme csak egyszer kerül tárolásra minden szintjén a fa, amelyből $ \ log n $. Ennélfogva, a teljes adatstruktúra vesz $ O (n \ log N) $ memóriát.
Klasszikus probléma a fán szegmense ez a típus az alábbiak szerint:
Mivel egy sor $ N $ szám, ami egy $ M $ lekérdezéseket. Lekérdezések formájában $ (l, r, x) $. Minden kérelmet kell válaszolni, hogy hány elem, nagyobb vagy egyenlő, mint $ x $, benne van a intervallumban $ [l; r] $.
A probléma megoldására lesz minden csomópont a fa magasságának tartani kiválogatott std :: vector. amely tartalmazza az összes elemet a megfelelő szegmensben. A válaszadást fogja használni az std :: LOWER_BOUND. Ez lehetővé teszi, hogy válaszoljon a kérelmet egyetlen csúcsa $ O (\ log N) $, így a teljes összetettségét a válasz a kérésre egyenlő lesz a $ O (\ log ^ 2 N) $.
Végrehajtás C ++:
Ha ilyen problémák lehet egy módosítását elemek, ahelyett, std :: vektor kell tárolni std :: MultiSet. amely lehetővé teszi, hogy gyorsan hozzá, törölhet tételeket. De ebben az esetben nem tudunk válaszoló számos elemet, mint iterátorokat std :: multiset nem veheti el egymástól.
Faelemek masszív frissítés. következetlen részfákat
Mivel bizonyos módosítások szegmens fa frissítés végrehajtásához elemek (növekedés vagy hozzárendelés) időközönként tetszőleges hossza a $ O (\ log N) $. Ez a módosítás meglehetősen gyakori, és megoldani segítségével a fadarabok egy osztály az új feladatokat.
Az ötlet a következő. Tegyük fel, hogy a tanfolyam a kijelölési kérelem intervallumon mentünk az első, teljesen tulajdonában ebben a szegmensben. Logikája szerint meg kell változtatni az értéket a tetején, és minden a tetejét a részfa. De a komplexitás egy ilyen művelet elfogadhatatlanul magas: $ O (n \ log N) $.
Ehelyett a következőképpen kell eljárni: a változó értéke csak a legtetején frissítése nélkül a részfa (tehát a részfa elavult hibás értékeket most tárolva), és emlékszem, hogy ez a csúcs koordinálatlan módosítását. Ebben a megkeresés a csúcson és a részfa befejeződött.
Ha későbbi kérések nem vonatkoznak részfa a jóváhagyott módosítás, akkor pontosan kell végrehajtani. De előbb-utóbb kérni kell feldolgozni egyedileg gyermek csomópontok következetlen módosítása. Ebben az esetben mi egyszerű: hogy a gyerekek a módosítás (csak másodlagos csúcsok, nem az egész al-fa). Most a tetején megállapodott, és eljuttatja a következetlenség az ő gyermeke. Ez a művelet a toló módosítását.
Talán, hogy feldolgozza a kérelmet csak akkor szükségesek gyermek csomópontok, és egy push elég lesz. Ha a kérés lent az al-fa, mivel ez nyomja az exponáló módosítás lejjebb és lejjebb. Pushing fut $ O (1) $ ugyanakkor megosztja a lekérdezés, ezért aszimptotikus viselkedését nem befolyásolja.
Tegyük fel például, hogy mi dolgozunk szegmense a fa, hogy megtalálja az összeg egy hatalmas feladat. Mi már kisajátított $ [0; 6] $ értéke $ x $. Változás az értéke az összeg a felső felelős ebben a szegmensben (állítsa $ 7x $), és a paraméter a vertex koordinálatlan módosítás egyenlő $ x $.
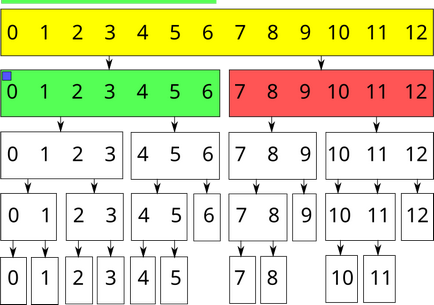
Kék négyzet jelenlétét jelzi egyező csúcsok módosítás.
Most mi lesz feldolgozni a kérelmet megállapítás összege $ intervallum [6; 7] $:
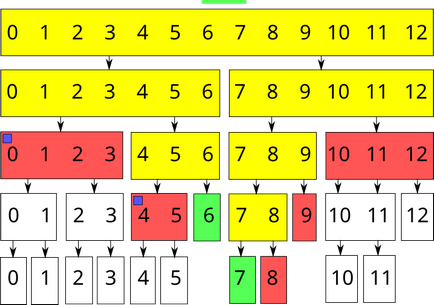
Mint látható, az ellentmondás átadott $ [0; 3] $ $ és [4; 5] $. Ő volna telt el, és a szegmens $ [6; 6] $, de nincs gyermek csomópontok, így az ellentmondás eltávolítjuk.