Fa szakaszok (bármilyen asszociatív funkció) Kód

A téma ezen a poszton - nem új, de minden bizonnyal hasznos valakinek :) Kezdjük egy példa a probléma, amely felhasználja a szegmens fa.

Van egy sor N (n≤10 ^ 5) egész számok, az összeg, hogy található az intervallum l R (0≤l, r≤n-1), és módosítsa az értéket a i-edik
(0≤i≤n-1) elem. Az m szám (m≤10 ^ 5) kérések.

Nyilvánvaló, hogy a naiv megoldás működik O (n * m), és a szegmens fa lehetővé teszi, hogy megoldja ezt a problémát az aszimptotikus O (m * log2n).

Sok különböző típusú szakaszok a fák. Ez a cikk szegmens fa - egy adatstruktúrát, amely szerint a rendelkezésre álló szekvenciát N szám lehet tenni gyorsan (logaritmikus idő) 2 féle lekérdezések:

1) módosítása az érték az i-edik eleme
2) Számítsa ki néhány fix asszociatív funkciók időközzel l r.

Ki az a szegmens, fa (a)? Ahhoz, hogy - bináris fa (általában, a kényelem kedvéért a komplement befejezéséhez nulla elemek), amelyek leveleit a forrás tömbben elemeket és minden csúcsában rögzített értékének az f függvény két fia. Azaz, a lap rögzített érték függvény az intervallum hossza 1, rögzítik a szülő a függvény az intervallum hossza 2, amelyben a szülő - 4 ... így rögzítve minden egyes vertex függvény értéke egy bizonyos intervallumban ez volt az oka ennek a neve.

A példánkban a feladat f függvény - összeget, akkor akár négy komponens a következő lesz:

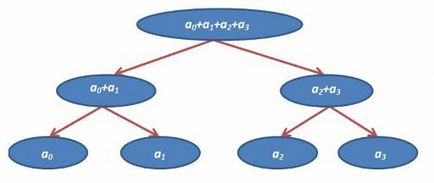
Ha van az elemek számát (n) nem kettő hatványa, akkor kiegészíti azokat nullákkal. (. Általában, amikor dolgozunk az adattípushoz T és egy f függvény, a pontszám - egy értéket úgy, hogy minden x T jobb f (x, nulla) = x), például, hogy összegezzük 3 elemek lehetnek:

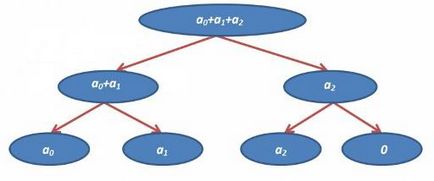
Hogyan tud tárolni? 2 módja van:
• szerkezet mutatók;
• lineáris tömb.

Amennyire én tudom, az első módszer csak az állandó UP. Mi is mindig elemzi a legtöbb hétköznapi és egyszerű módosításával, így a második módszer. Készítsen egy lineáris tömb 2 * Nmax elemek, ahol Nmax - a legkisebb erő a két, amely nem haladja meg a n. Az első elem (a [1]) tárolja a gyökér a fa, és minden v csúcsra i fiait tárolt sejtek számozott 2 * i (bal fia) 2 * i + 1 (jobb fia). Miért van ahhoz, hogy tárolja a 2 * Nmax elemeket? Van nmax lapokat, akkor Nmax / 2 szülő, akkor Nmax / 4 ... és 1 gyökér, egyértelmű, hogy ez az összeg (1 + 2 + 4 + ... + Nmax / 4 + Nmax / 2 + nmax) = 2 * Nmax -1.

Az ábra letette közel minden csúcsa az index a tömbben:

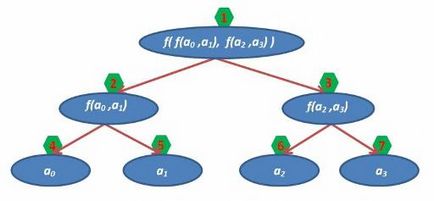
És tömörfa kerül bemutatásra az alábbiak szerint:

Most határozzuk meg, hogy milyen műveleteket szeretnénk végezni a TO:
1) építésére;
2) ismerik a értéke az i-edik eleme;
3) módosítsa az értéket a i-edik eleme;
4) funkciót találni az értéket az intervallum l r.

Nézzük egyenként a műveleteket.

1. Készítsen egy fa szegmens.

Tegyük fel, hogy egy sor n elemek b. Először meg kell találnunk Vmax (a legkisebb teljesítmény, hogy a két nem nagyobb, mint n). Ez megvalósítható akár a képlet:

és szerény ciklus:

Ezenkívül igény, hogy kitöltse a tömb nullákkal (megfelelő típusú), és töltse lapok tömb elemeinek b (arra gondolunk, hogy a indexek a levelek nmax a 2 * Nmax-1):

Abban a pillanatban, van:

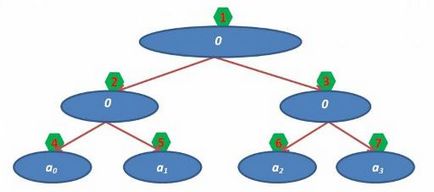
Most már csak ki kell töltenie értékeket minden szülő. Ezt meg lehet tenni egy egyetlen lineáris átjáró (emlékezni, hogy az i-edik csúcsból fiai indexű 2 * i és 2 * i + 1, és a vertex tárolunk értékét függvényében két fia):

Így már épített aszimptotikus O (nmax) = O (n).

2. Keresse ki az értéke az i-edik eleme.

Amint azt már korábban a TO levelek indexek nmax 2 * max-1, így az értéke az i-edik eleme az elem a sejtben egy index Nmax + i: visszatérés a [nmax + i] Nyilvánvaló, hogy a lekérdezés lefut az állandó .

3 Módosítsa az értéket az i-edik eleme.

Ha megváltoztatjuk az értéket a levél a fa, az összes értéket a módja, hogy a gyökér egy adott lemez már nem lesz igaz, ezért kell számítani, de egyébként továbbra is a helyes értékeket. Mint ismeretes, a mélység a teljes bináris fa m csúcsok log2M, így kénytelenek vagyunk művelet elvégzéséhez logaritmikus időben. Például egy változás a2 a2:

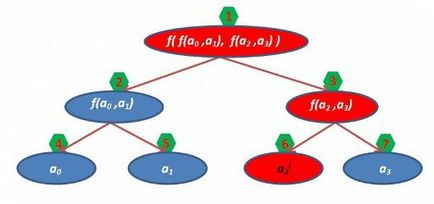
Pirossal kiemelve top, ahol meg kell változtatni az értékeket.

Mi lenne a „frissítés” meg kell adni a listához egy új értéket, majd felmászni a gyökér, minden egyes alkalommal számítva a függvény értéke a tetején. Módosítsa az értéket a lap nagyon könnyű (ne feledjük, hogy indexek indul nmax 2 * max-1). Az érték az i-edik lap rendelkezik egy indexet Nmax + i:

Most, hogy menjen fel a gyökér, hogy meg lehet csinálni egy hurok:

4. Keresse meg függvény értékét az intervallum l r.

Végül elértük a legérdekesebb kérelmet. Meg kell jegyezni, hogy a speciális esetben, amikor L = r analizáltuk a 2. lépésben, és végezzük állandó, az általános esetben, a logaritmikus aszimptotikus.

Alapvető szegmens - a szegmens, ahol van egy csúcs a fa, amely tartja az értékét a függvény egy adott intervallumban.

Szint. gyökér szinten - 1, és minden fiai szinten az egyik nagyobb, mint a szülő.

Annak érdekében, hogy kiszámítja a függvény értékét az intervallum, meg kell osztani azt a legkisebb számú elemi szegmensben. Ahhoz, hogy megtalálja az értéket minden csúcsa (kivéve papíron), tudnunk kell, hogy az értékeket a fia. Mi leereszkedünk. Kezdetben emelkedik a gyökér. Tegyük fel, hogy van valamiféle tetején. Tekintsük a 3 lehetséges eset van: szegmens [l..r] egybeesik a szegmens megfelelő a jelenlegi csúcs, a szegmens [l..r] tartozik teljesen az egyik gyerek, a szegmens tartozik mindkét fia. Az első esetben, csak vissza a számlálási érték a PTE, a második - le, hogy ez a fia, osztjuk ezt a szegmenst két harmada az ugyanazon esemény: [l..pravy végén a bal fia] és [bal végén jobbra syna..r]. Rekurzívan kiszámítja értékeket mindegyik.

Tekintsük a következő példát. Tegyük fel, hogy a 8 elemet írunk, amely megfelel a hossza az egyes vertex:

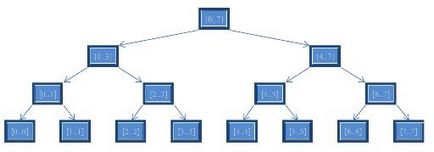
Most nézzük meg, hogyan fog végezni a kérelem intervallum [1..5].

Először is felkelni, hogy a gyökér - a szegmens tartozik mindkét fia. Tehát szükségünk bonthatjuk 2 részes: [1..3] és [4..5]. Mert mindegyikük rekurzív kiszámolja az értéket. Továbbá, az intervallum [1..3] 2 ismét tartozik fiai, osszuk két szegmens: [1..1] és [2..3]. Az intervallum [1..1] tartozik csak a megfelelő gyermek, hogy le, és látni, hogy a [1..1] - alapvető fontosságú. Az értéke annak a felső, és emelkedik fel a 2. szintű (csúcs [0..3]). A bal oldalon van egy fia rekurzív tekinteni most számolja a jobb: menjen le vele. Az intervallum [2..3] - alapvető, hogy egy értéket a tetején. Megyünk vissza a [0..3], ezért már az A értékét az intervallum [1..3], mivel a függvény értéke már számított két részből áll. Menj vissza a gyökér és leereszkedünk a jobb gyermek [4..7], a mi szubszegmentum ([4..5]) tartozik, hogy csak egy fia elhagyta leszállnak bele. Vertex felel meg, az [4..5], ezért - az alapvető, hogy értéke a csúcs. Megyünk vissza a gyökér és kiszámítani a választ.

Miért van ez a lekérdezés végrehajtásra logaritmikus időben? Mint ismeretes, a mélység (szintek száma) a fa az n csúcsú egyenlő log2n, továbbá azt állítják, hogy minden szinten megtekintjük, hogy 4 csúcs, ezért keresse fel O (log2n) csúcsok. Tekintsük a kódot. Értékének kiszámításához a szegmens, szükségünk van egy rekurzív függvényhívás érvek 5 kedvéért írunk funkció, hogy a 2 érvek (a lekérdezés szegmenshatáraival) 5-és függvényargumentumok és visszaadja az értéket:

Most a rekurzív függvény:

Saját osztályú fa kód szegmens egyetlen módosításra.

Ui Én szívesen konstruktív megjegyzéseket / javaslatokat írásban cikkek / code

részes fa. képek. kódot. részes fa