Kiszámítása matlab
MATLAB nyújt a különböző módszerek megoldására differenciál-és integrálszámítás, oldatok differenciálegyenletek bármilyen fokú és kiszámításának korlátok. A legjobb az egészben, akkor könnyen építeni bonyolult grafikák funkciók és tesztelje a magasságra, mélypontra került, és egyéb irodaszer pont a grafikonon megoldása az eredeti funkció és a származékos.
Ez a fejezet foglalkozik a problémákat a fogkő. Ebben a fejezetben tárgyaljuk előzetes számítása a koncepció, hogy kiszámításakor határait funkciók és ellenőrzi a tulajdonságait korlátokat.
A következő glavedifferentsial, kiszámítjuk a származékos kifejezési és megállapítás helyi maximumok és minimumok a grafikonon. Azt is megvitatják a megoldásokat differenciálegyenletek.
És végül, a glaveintegratsii, megbeszéljük a integrálszámítás.
határértékeinek kiszámítására
Obespechivaetpredelnuyu MATLAB függvény kiszámítására korlátokat. A legalapvetőbb formája, a végső kifejezése a függvény argumentumként, és megállapítja a határ a kifejezés. mint a független változó nullához.
Például, kiszámítjuk a határértéket a függvény F (x) = (x 3 + 5) / (4 + x 7), ha x nullához.
MATLAB végrehajtja a fenti nyilatkozatot, és visszatér a következő eredmény -
A limit funkció esik a terület szimbolikus számítások; meg kell ispolzovatSyms funkció MATLAB. szimbolikus változók. használja. Ezen kívül lehet számítani a határ a funkciója, mint a változó hajlamos számos más mint nulla. A számításhoz az Rm x> a (P (x)), akkor használja a limit parancs érveket. Először. amely expressziós. és a második szám, hogy x megközelítések, itt vagyunk.
Például, kiszámítjuk a határértéket a f (x) = (X-3) / (1-x), amikor x közelít 1.
MATLAB végrehajtja a fenti nyilatkozatot, és visszatér a következő eredmény -
Vegyünk egy másik példát,
MATLAB végrehajtja a fenti nyilatkozatot, és visszatér a következő eredmény -
Kiszámítása határok alkalmazásával Octave
Az alábbiakban Octave változata a fenti példa. ispolzuyasimvolichesky csomag, próbálja ki és hasonlítsa össze az eredményeket -
Octave elvégzi a fenti állítás, és visszaadja a következő eredmény -
Ellenőrzése alapvető tulajdonságait Limits
Algebrai határeloszlás néhány alapvető tulajdonságait korlátokat. Ezek az alábbiak -
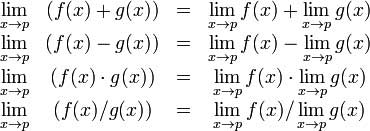
Tekintsük a két funkció -
Kiszámítjuk a határait a függvény x hajlamos 5, a két funkció, hogy ellenőrizze az alapvető tulajdonságait a határait a két funkciót és a MATLAB.
Hozzon létre egy script fájlt, és adja meg az alábbi kódot, hogy -
Ha a fájl futtatásához, akkor megjelenik -
Ellenőrzés alaptulajdonságait határértékek alkalmazásával Octave
Az alábbiakban Octave változata a fenti példa. ispolzuyasimvolichesky csomag, próbálja ki és hasonlítsa össze az eredményeket -
Octave elvégzi a fenti állítás, és visszaadja a következő eredmény -
A bal és jobb oldali korlátokat
Amikor a funkció rés van néhány konkrét értékekhez, a határérték nem létezik ezen a ponton. Más szóval, a határ a függvény F (x) van egy folytonossági hiány x = a, amikor a határérték x hajlamos x a bal oldalon nem egyenlő a határérték x közeledik a jobb oldalon.
Ez ahhoz vezet, hogy a koncepció a bal és jobb határokat. Lefty határérték kerül meghatározásra a határérték x -> egy, a bal oldali, azaz X megközelítések és, az x értékei <а. Правый предел определяется как предел при х -> és a jobb oldalon, azaz, x közelít a x> és értékeit. Amikor a bal és jobb limit limit nem egyenlő a határérték nem létezik.
Megmutatjuk. hogy lim x> 3, E (x) nem létezik. MATLAB segít létrehozni ezt a tényt két módon -
- Ezzel a rajzoló funkciókat, és bemutatja a különbség.
- A számítás a korlátokat és azt mutatja, hogy ezek mind különbözőek.
A bal és a jobb felső határértékeket kiszámítják egy karaktersorozatot át „hogy a bal” és „jobb”, hogy korlátozza a csapat, mint az utolsó érv.
Hozzon létre egy script fájlt, és adja meg az alábbi kódot, hogy -
Ha a fájl futtatásakor MATLAB felhívja a következő telek
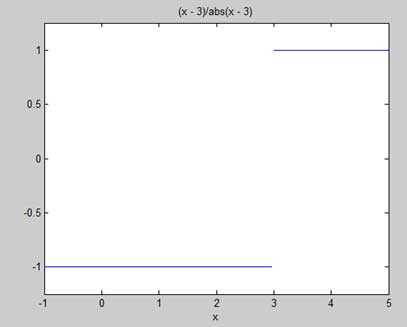
Amint megjelenik az alábbi következtetést -