A számla a saját súlya
A feszültség a prizma rúd
Nettó tömeg kiszámításához feszültség-alakváltozás elszámolni konstrukciók, amelynek tömege összemérhető az értékeket külső terhelés. Ez az oszlop lehet erősíteni, tégla válaszfalak és mások.
Tekintsük a belső erők és feszültségek a feszített rúd alatt egyidejű hatása koncentrált erőt $ F $ és a saját súlyát. Súly úgy definiáljuk, mint a rúd
$ Q = \ gamma \ cdot V = \ gamma \ cdot A \ cdot l $,
ahol $ \ gamma $ - konkrét anyag súlyát [kN / m 3], $ V $, $ A $, $ l $ - egy „térfogatú keresztmetszeti terület és hossza bár, ill. Fajsúly FL „társított anyag sűrűsége $ \ gamma = g \ cdot \ rho $, ahol $ g \ kb $ 10 m / s 2. $ \ rho $ - sűrűség.
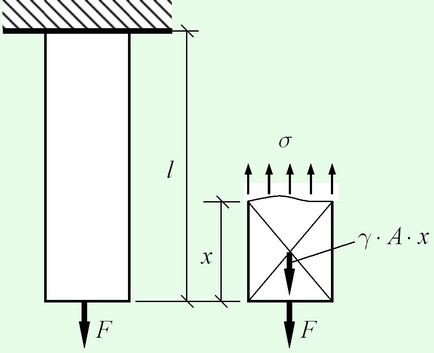
A hosszirányú erő fordul elő, hogy a szakasz és - És
$ N = F + \ gamma \ cdot A \ cdot x $
A feszültség a fiók a saját súlya
$ \ Sigma = \ frac = \ frac + \ gamma \ cdot x $
A legnagyobb stressz akkor a felső rész és a szilárdsági feltétel formájában
$> = \ Frac + \ gamma \ cdot l \ leqslant \ left [\ sigma \ right] $
Válogatás a keresztmetszeti területe tekintettel a saját súlya
Brus egyenlő ellenállás
Beam nevezzük gerenda egységes erő, ahol a feszültség nem változik, és a hossza általában megegyezik megengedett feszültség.
Érthető, hogy megfeleljen ezeknek a feltételeknek, a gerenda keresztmetszeti területe függően kell változnia a változás a hosszirányú erő. Nézzük meg egy végtelenül eleme a gerenda (ábra). A hossz $ dx $. Az alsó rész az elem területe $ A $. Hosszirányú erő ez $ [\ sigma] \ cdot A $. A hosszanti irányú erő a felső szakasz nőtt a súlya a elem értékét, azaz, $ dN = \ gamma \ cdot dV = \ gamma \ cdot A \ cdot dx $. Ennek megfelelően a terület megnövekszik az összeg $ dA = \ frac >> $.
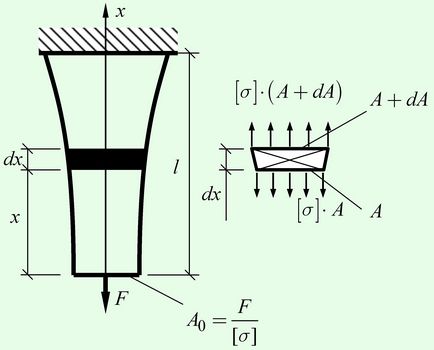
$ DN = \ gamma \ cdot A \ cdot dx = dA \ cdot [\ sigma] $,
Az alsó részben, ahol a hosszirányú erő $ N = F $, keresztmetszeti terület legyen
Azaz, hogy ugyanazt a stressz hossza mentén a rúd keresztmetszeti területe függően kell változnia a exponenciális függés
lépcsős gerendák
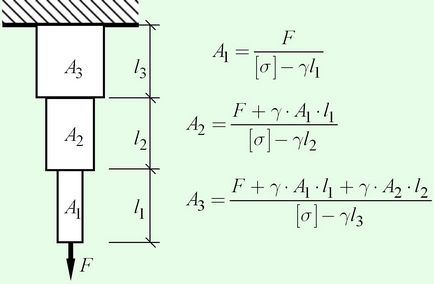
Beam egységes erő kényelmetlen gyártani, így a stressz kiegyenlítési segítségével lépésváltásra keresztmetszete a hossza mentén. A száma és hossza lépések meghatározása függ a helyzetet, és a szükséges keresztmetszeti területe minden egyes szakaszában előírt feltételek erőt egy hasáb alakú fa. Például, egy háromfokozatú gerenda egy terhelés a végén a számítás a keresztmetszeti területe a huzal, amint azt a 6.3 ábra.
Deformáció saját súlya alatt
Feszültség, figyelembe véve csak a saját súlya a hasáb alakú gerendából
Ha a rúd, kivéve a saját súlyuk $ Q $ erő az F $ $, nyúlást fogja meghatározni a következő képlettel
Deformációja azonos erősségű sugár határozza meg könnyebb, mert a feszültség minden részében azonos $ \ sigma = \ left [\ sigma \ right] = const $, majd a Hooke-törvény
$ \ Delta l = \ varepsilon \ cdot l = \ frac> \ cdot l $