Határozza meg a sűrűsége egy gömb alakú bolygó, ha a súlya a test a pole 2-szer nagyobb
Állapota a problémát:
Határozza meg a sűrűsége egy gömb alakú bolygó, ha a súlya a test a pole 2-szer nagyobb, mint az egyenlítő. Az az időszak, a Föld forgása a tengelye körül 2 óra 40 perc.
№2.5.15 feladata a „Collection feladatok előkészítése a felvételi vizsgák a fizika UGNTU”
Megoldás:
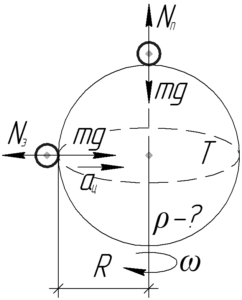
A test a pole fekszik a forgástengely a bolygó, ezért forog csak körülöttük. Newton első törvénye erre szerv adja ezt az egyenlőséget:
Newton harmadik törvénye, a padló reakció erő (\ (N_e \) és \ (N_p \)) egyenlő testtömeg (\ (P_e \) és \ (P_p \) rendre). Vegye figyelembe, hogy ezek az erők, de azonos nagyságú, de ellentétes irányú és alkalmazni a különböző szervek. Ezt szem előtt tartva, írhatunk egyenlet (1) és (2) az ilyen rendszerben:
Osszuk az alsó egyenlőség a tetején. Mivel a \ (P_p 2P_e = \), megkapjuk:
Mivel a probléma kell tudni az átlagos sűrűsége a bolygó \ (\ rho \), majd írjuk ilyen formulák: először is, a képlet meghatározására gyorsulás szabadesés \ (g \) a felületen, másrészt a képletet meghatározó súlya a sűrűség és térfogat, Harmadszor, a képlet meghatározására kötet egy gömb.
Behelyettesítve (6) be (5), a kapott (4), kapjuk:
Ahhoz, hogy kifejezze a centripetális gyorsulás \ (a_ts \) forgatásával a bolygó időszakban \ (T \) levelet ilyen formulák: képletű gyorsulás detektálás \ (a_ts \) keresztül szögsebesség \ (\ omega \) és kommunikációs képletű utóbbit egy időszakra forgási \ (T \ ).
Helyettesítse a kifejezések (7) és (8) előzőleg kapott (3) egyenlet:
Fordítás a rotációs időszak abban az állapotban \ (T \) SI mértékegység (másodpercben):
\ [T = 2 \, H \, 40 \; m = 2 \ cdot 3600 + 40 \ cdot 60 \; c = 9600 \; c \]
A: 3,07 g / cm 3.
Ha tetszik a probléma és annak megoldása, akkor ossza meg ismerőseivel Ezekkel a gombokkal.