A gravitáció törvénye, az elmélet és az online kalkulátorok
Az elején a XVII században a heliocentrikus rendszer a világ által elismert legtöbb tudós. Azonban abban az időben nem volt egyértelmű okokból, valamint a törvényeket, amelyek a bolygók.
Kepler feldolgozta az eredményeit, sok észrevételt és kollégája T. Brahe, fogalmazott a törvények a mozgás a bolygók a nap körül. Világossá vált, hogy annak érdekében, hogy ismertesse Kepler törvényei, meg kell határoznia, milyen erők hatnak a bolygón. De Kepler és kortársai nem tudta végrehajtani azt. Problémát úgy oldották meg Isaac Newton.
Körülbelül, akkor feltételezhetjük, hogy a bolygók mozgott egyenletesen kering közel a köröket. Az ilyen típusú részecske mozgás van egy centripetális gyorsulás, amely arra irányul, közepe felé a pályára (a bolygó, a centripetális gyorsulás irányul, hogy a Sun). Newton második törvénye azt jelenti, hogy a bolygó néhány erőt alkalmaznak, amely okot ad a normál gyorsulás. Kiderült, hogy a Nap jár minden bolygón erővel a középpont felé. Szerint a Newton harmadik, a bolygó hat nap erővel egyenlő nagyságú erő az előző, de mivel az ellenkező irányba.
Az egyetemes tömegvonzás törvénye
Tudjuk, hogy a hold forog a Föld körül. A hold vonzza a föld, a föld vonzza a hold. Newton azt javasolta, hogy a gravitáció, amellyel a Föld vonzza minden testek felszíne közelében, és az erő, amellyel ez vonzza a Hold azonos eredetűek. Newton képest gravitációs gyorsulás ($ g = 9,81 \ \ frac> $ közelében a Föld felszínét) és a centripetális gyorsulás ($ a_n $), amelynek van egy hold, amikor mentén mozgó pályáján. Newton volt, hogy a gyorsulás a Hold egyenlő $ a_n = 2,72 \ cdot ^ \ frac $. Az eltérés az értékek Newton azzal a ténnyel magyarázható, hogy a gravitációs erő csökken a távolság növelésével között vonzó testek. A gyorsulás okozta gravitáció, fordítottan arányos a távolság négyzetével ($ r $) szervek közötti:
A megfogalmazás a gravitáció törvénye
Elemzés a normál gyorsulás a Hold, ahogy mozog a Föld körül hagytuk Isaac Newton arra a következtetésre, hogy az összes szervek jellegű vonzódnak bizonyos erők, amelyek az úgynevezett gravitációs erők.
Tegyük fel, hogy van két test, amelyeknek tömege egyenlő m_1 $ $ és $ $ m_2. Ezek található a parttól $ r $ egymástól. Ezek a testületek kölcsönhatásba erők:
Szerint a Newton harmadik van:
Figyelembe véve az (1) kifejezés, megkapjuk:
Expression (4) teljesül, ha a $ K_1 = \ gamma m_2, $ a $ K_2 = \ gamma m_1, $, ahol $ \ gamma $ = const. Azaz, azt találtuk, hogy:
Az (5) - a matematikai kifejezése a gravitáció törvénye: A gravitációs erő két lényeges ponton egyenesen arányos a tömegek és fordítottan arányos a tér a távolság közöttük.
A pontos kiszámítása a vonzó- (5) képlet csak akkor alkalmazható, ha a testek homogén golyók, amelyeknek tömege egyenlő m_i $ \ m_2 $, és $ R $ - közötti távolság a központ.
gravitációs állandó
A relatív $ \ gamma $ nevezzük gravitációs állandó. A Nemzetközi Mértékegység Rendszer (SI) ez egyenlő a $ \ gamma \ kb 6,67 \ cdot ^ \ frac. \ $ Gravitációs állandó értéke számszerűen egyenlő az erő közötti kölcsönhatás lényeges pontokon tömegek egy kilogramm található, a parttól egy méter. A gravitációs állandó Kísérletileg.
Az egyik első kísérlet mérni a gravitációs erő a laboratóriumban meghatározott Cavendish. Így meghatározzuk a gravitációs állandó.
Példák problémák megoldás
Feladat. Mi a lényege a Cavendish kísérlet mérni a gravitációs erő?
Határozat. Készíts egy rajzot.
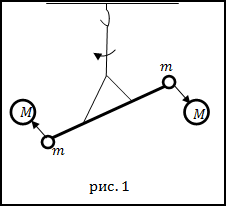
A kísérlethez a Cavendish kísérletben használt a torziós inga (1. ábra). Egy vékony kvarc szál felfüggesztett könnyű bot. A menet mereven tartott egy kis tükröt. A fénysugár esik a tükör, tükröződik belőle, és esik a skála. Ha a rúd forog, a sugár mentén mozog a skála. Mivel a csavar szög a menet volt megfigyelhető. A végén a rúd van rögzítve két golyó ólom, egyenként $ m $. Ezek a golyók tálca két szimmetrikusan elhelyezett labda ólom tömegek $ M $. Menet forgatni, amíg a rugalmas erő a deformált szálat kiegyensúlyozza az erő a gravitációs kölcsönhatás a golyókat. A kölcsönhatás erősségét mérjük a szög sodratú. Ismerve a súlya a golyók és a távolság közötti központok, számítjuk a gravitációs állandó.
Feladat. Két azonos homogén vas labdát érintés egymással (2. ábra). A sugár egyes golyók egyenlő $ R = 0,1 $ m. A gravitációs erő hat a labda?
Határozat. Készíts egy rajzot.
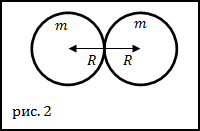
Az alapot a megoldás a problémára az egyetemes tömegvonzás törvénye:
ahol $ m_1 = m_2 = m $ - tömege mindegyik labda, akkor a gravitáció törvénye felírható:
A központjai közötti távolság a golyók (2. ábra) egyenlő :. $ R = 2R $ súlyok megtalálják golyó, mint:
\ [M = \ rho \ frac \ pi R ^ 3 \ bal (2,3 \ jobbra). \]
(2.2) transzformálására a következőképpen:
Kiszámításához a gravitációs erő, találunk könyvtárak vas sűrűsége ($ \ rho = 7800 \ \ $ frac). A gravitációs konstans: $ \ gamma = 6,67 \ cdot ^ \ frac $ elvégzi a számítást .: