Az arc tg és inverz kotangens
19. § Arc érintő és inverz kotangensét. TGX egyenletek megoldása = a, ctgx = egy
A 2. példában §16, nem tudtuk megoldani a három egyenletet:
Kettő közülük már döntöttek - az első 17. § és 18. §-a második, tenni, hogy mi volt a koncepció a arkusz és arkusz szinusz. Tekintsük a harmadik egyenlet x = 2.
Funkciók Charts = tg y x = 2 és y végtelen sok közös pontja, az abszcisszán az összes ezek a pontok a formában - az abszcissza a metszéspontja a vonal y = 2, azzal a fő ága tangensoidy (90. ábra). A szám x1 matematika jelölést feltalált agstg 2 (ejtsd „cotanges két”). Ezután minden gyökerei az egyenlet x = 2 leírható a következő képlettel: x = 2 + agstg PC.
Mi agstg 2? Ez - szám, amelynek érintője 2, és amelyik az intervallum
Tekintsük most az egyenletet tg x = -2.
A grafikonok funkciókat végtelen sok közös pontja, abszcisszájának mindezen pontok formájában van jelen abszcissza a metszéspontja az y = -2 tangensoidy a fő ága. A szám x2 matematikai jelöléssel feltalált agstg (-2). Ezután minden gyökerei az egyenlet x = -2 leírható a következő képlettel
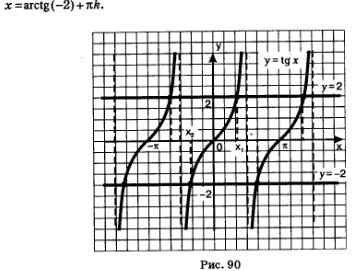
Mi agstg (-2). Ez az a szám, melynek tangense egyenlő -2, és amely tartozik a intervallumot. Megjegyzés (lásd 90. ábra ..): X2 = x2. Ez azt jelenti, hogy agstg (-2) = - 2 agstg.
Meghatározó cotanges megfogalmazni általánosságban.
1. meghatározása agstg a (cotanges a) - egy szám az intervallum. melynek tangense egyenlő a. Így
Most tudjuk, hogy általános következtetéseket levonni a döntést az egyenlet x = a és x = egyenlet megoldások
Fent említettük, hogy a agstg (-2) = -agstg 2. Általánosságban, bármely értéke érvényes általános képletű
1. példa kiértékelése:

2. példa: oldja egyenletet:
Megoldás: a) felállított képlet készítés:
A értékét az arkusz tangens ebben az esetben nem tudjuk, ezért hagyja nyilván a megoldás, ahogy kaptuk.
válaszolni:
3. példa megoldásához egyenlőtlenséget:
egyenlőtlenség lehet oldani grafikusan, azért, hogy a következő terv
1) építeni tangensoidu y = tg x és az y = A;
2), hogy azonosítsa a fő ága tangeysoidy intervallum X tengely, amelyen az előre meghatározott egyenlőtlenség;
3) figyelembe véve a periodicitás a függvény y = tg x, írja a válasz általános módon.
Ez a terv alkalmazható a megoldás halmaza egyenlőtlenségeket.
Határozat. a) konstrukció a grafikon y = TGH és y = 1. A fő ága tangensoidy ezek pontban metszik egymást
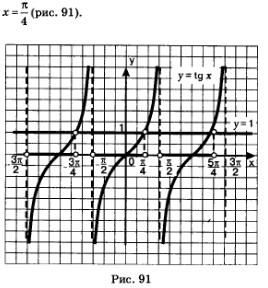
Isolate intervallum x tengelyen, ahol a fő ága tangensoidy alatt található egyenes y = 1, - az az időköz
Mivel a frekvencia függvény y = TGH, arra a következtetésre jutunk, hogy az egyenlőtlenség van megadva minden intervallum formájában:
A Union az összes ilyen intervallumok, és egy általános megoldás, hogy egy előre meghatározott egyenlőtlenség.
A válasz lehet írni más módon:
b) építünk a grafikon y = tg x és y = -2. A fő ága tangensoidy (ábra. 92), azok metszik a ponton x = agstg (-2).
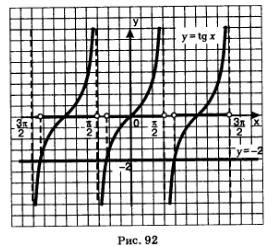
Isolate intervallum x tengelyen, ahol a fő ága tangensoidy
Tekintsük az egyenlet tg x = a, ahol a> 0. Grafikon funkciók y = CTG x és y = a végtelen sok közös pontot, az abszcisszán az összes ezek a pontok a formában: X = X1 + nk ahol X1 = agsstg és - az abszcissza a metszéspont az egyenes y = a a fő ág tangensoidy (93. ábra. ). Ezért agsstg egy - egy szám, amely egyenlő a kotangensét a és amely tartozik a (0, n); ez az intervallum épül a fő ága a grafikon y = x CTG.
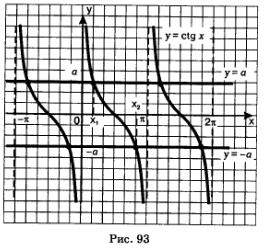
Ábra. 93 ábra szemlélteti grafikusan megoldások és s1tg = s egyenlet. Funkciók Charts CTG y = x és y = -a végtelen sok közös pontot, az abszcisszán az összes ezek a pontok az x = x2 + nk ahol agsstg x2 = (- a) - az abszcissza a metszéspontja a vonal y = -a fő ága tangensoidy . Ezért agsstg (ek) - egy szám, amely egyenlő a kotangensét megadott, és amely tartozik a intervallum (O, N); ez az intervallum épül a fő ága a grafikon y = x CTG.
2. Meghatározás agsstg egy (inverz kotangensét a) - egy olyan szám, a (0, n), amely egyenlő a kotangensét a.
Így
Most képesek vagyunk általánosítani CTG egyenletek megoldására x = a: CTG egyenlet x = van egy megoldás:
Megjegyzés (lásd 93. ábra ..): X2 = x1 n. Ez azt jelenti, hogy
4. példa Számítsuk:
Megoldás: a) Legyen
CTG egyenlet x = a majdnem mindig lehet alakítani kivételével az x = 0 CTG. De ebben az esetben, az a tény, hogy akkor megy
egyenlet cos x = 0. Így, az egyenlet az x = önálló nem érdekelt.
AG Mordkovich Algebra 10. évfolyam
Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.
Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.