Tulajdonságok funkciók folyamatos intervallumon
Definíció. Ha az f (x) meghatározott a [a, b], a folyamatos, minden pontján az intervallum (a, b), egy jobbról folytonos a b pont folyamatos a bal oldalon, azt mondjuk, hogy az f (x) folytonos a [a, b].
Más szóval, az f (x) folytonos a [a, b], ha az alábbi három feltétel:
Mert funkciókat, amelyek folytonos az intervallumon, úgy bizonyos tulajdonságait, amelyek megfogalmazzuk az alábbi tételek lefolytatása nélkül bizonyítékokat.
Tétel 1. Ha az f (x) folytonos a [a, b], akkor éri el a szegmensét a minimális és a maximális értéket.
Ez a tétel kimondja, (ábra. 1,15), hogy a [a, b], létezik egy pont x1. hogy f (x1) ≤ f (x) minden x a [a, b], és hogy van egy pont x2 (x2 [a, b]) oly módon, hogy
Értéke az f (x1) a legnagyobb egy adott funkciót [a, b], és az f (x2) - legkisebb. Legyen: f (x1) = M, F (x2) = m. Ami a f (x) kielégíti az egyenlőtlenséget :. megkapjuk az alábbi következmény 1. tétel.
Következmény. Ha az f (x) folytonos a, ilyenkor csak ebben az intervallumban.
Tétel 2. Ha az f (x) folytonos a [a, b] és a végpontokban veszi értékeit a különböző jelek, akkor van egy belső pont x0 [a, b], amelyben a függvény értéke 0, azaz, .
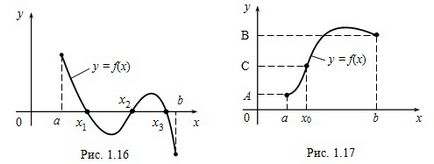
Ez a tétel kimondja, hogy a függvény grafikonját y = f (x), folytonos az [a, b], metszi Ox tengelyt legalább egyszer, ha az értékek a F (a) és f (b) ellenkező előjelű. Például, (ábra. 1,16) f (a)> 0, F (b) <0 и функция f(x) обращается в 0 в точках x1. x2. x3 .
3. tétel Legyen az f (x) folytonos a [a, b], f (a) = A, F (b) = B, és
A ≠ B (ábra. 1.17). Ezután, tetszőleges számú C, között a számok A és B, létezik egy belső pont x0 [a, b], hogy f (x0) = C
Következmény. Ha az f (x) folytonos a [a, b], m - a legkisebb érték az f (x), M - a legmagasabb érték az f (x), az [a, b], akkor a függvény (legalább egyszer) bármelyik értéke m, zárt m és m között, és így a [m, m] a készlet minden függvény értékei az f (x), az [a, b].
Megjegyzendő, hogy ha a függvény folytonos a (a, b), vagy az intervallum
[A, b] az a pont a diszkontinuitás, tételek 1, 2, 3 ilyen funkciók már nem érvényes.
Végül úgy véljük, az elmélet létezését inverz függvényt. Emlékezzünk vissza, hogy egy rés értetődő az intervallum, vagy időközönként véges vagy végtelen intervallumban.
4. Tétel Legyen f (x) folytonos a X, növekszik (vagy csökken) a több X és Y. Ezután az intervallum-értékeket a függvény y = f (x) egy inverz függvény x = # 966; (y), meghatározott intervallumon Y, folyamatos és növekvő (vagy csökkenő) az Y a beállított értékek X.
Megjegyzés. Legyen a függvény x = # 966; (y) az inverz függvény f (x). Amint általában jelöli az érv x, és a függvény által y, akkor tudjuk írni a inverz függvényeként y = # 966; (x).
1. példa A funkció y = x 2 (ábra. 1,8, a) egy sor, az X = [0, + ∞) folyamatos, növekvő és sokasága van az Y = [0, + ∞). A függvény az y = x 2 az inverz függvény x = √y (ábra. 1.8, b), és miután az átnevezés változók y = √x. Különösen, folyamatos és növekvő X.
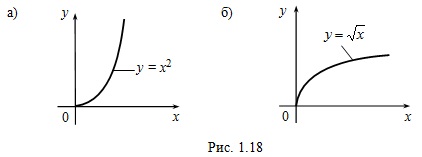
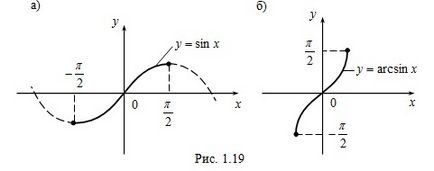
2. példa A funkció y = sinx (ábra. 1,19, a) folyamatos és növekvő az intervallumot, és több, az [-1, 1] értéket, így azt a inverz függvényeként y = arcsinx (ábra. 1,19, b) egy adott, a folyamatos és növeli az intervallum [-1, 1] és amelynek több értékek
Megjegyezzük, hogy a grafikonok az inverz funkciók szimmetrikus vonal y = x. Kínálunk a telek kölcsönösen inverz funkciók:
1. y = cosx, y = arccosx;
2. y = TGX, y = arctgx;
3. y = ctgx, y = arcctgx;
4. y = e x. y = LNX.