tulajdonságai határértékek





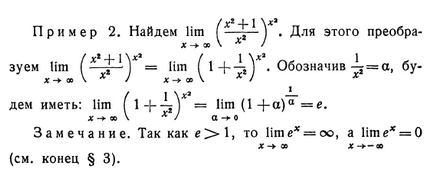
Tulajdonságai határértékek minden példát, amelyeket a fenti, nem találtunk a korlátokat, és azt állította, hogy egy ilyen szám a határ egy adott funkció ilyen körülmények között. A kérdés természetesen felmerül, hogyan találjuk meg a számot, amelyre mi továbbra is azt állítja, hogy a határ az adott funkciót. Ez a probléma szinte mindig nagyon nehéz, különösen akkor, ha jön egy bizonyos határértéket. Ahhoz, hogy ezt a feladatot segíti általában használ bizonyos tulajdonságait korlátozza a bemutatása, amely most viszont. Említett tulajdonságokat magyarázható példák és bizonyítékok nem adható. Bizonyíték megtalálható még teljesebb tanfolyamok, mint például: Piskunov NS „Megkülönböztető és integrálszámítás” vagy Tarasov, NP „Természetesen a magasabb matematika.” Tulajdonság 1. A határérték mennyiségű bizonyos funkciók egyenlő az összege határértékek minden egyes ilyen funkciók, azaz. E. Lim [/ (*) + q> (*)] «IX / (*) + líra. X - * -, és X és X -a A készítmény az ingatlan, valamint az alábbi, azt feltételezzük, hogy az összes határértékek kiszámítása át azonos körülmények között. Példa 1. Keresse lim
sin * t tudja, hogy X X megjegyzésben. A készítmény tulajdonságainak 1 összességére utal, de mivel a különbség mindig felírható az összeg az ingatlan kiterjed 1 különbséget. sin x-x * példa 2. Keresse meg a lim -. X O * = As + xn), majd alkalmazása ingatlan 1, megkapjuk lim lim X - * - O * X - + Q L J L Tulajdonság 2. A határérték funkció, amely megtartja ugyanazt az értéket, egyenlő ezt az értéket. Ez a tulajdonság megfogalmazott eltérő módon: a határ a konstans, hogy állandó. 3. példa Nézzük lim [sin ** + cos * x]. i X - 2 Mivel sin * x - \ - cos * x minden értékére x egyenlő 1, van olyan eset, amikor egy állandó értéket, így lim [sin * x + cos * x] = 1. £ 1 - g 4. példa találunk lim 7,5. Mivel x 7,5 posto-
* -x szíthet és nem függ x, akkor lim 7,5 = 7,5. X és ingatlan 3. Limit A termék két funkció a termék határain ezeket a funkciókat. T-ze és X * sin x 4- sin * X 5. példa Tegyük lim -j-. X -> x az 1. példa E szakasz, kimutatták, hogy a lim - = 1, és 2. §-ban -, hogy lim = 1. Az X - + Q X X - * - Q tulajdonság X 3, megkapjuk x * sin x -f sin * x * YX -f sin x sin x
\ Lim X - t. X9 + sin sin * *. t = lim --- lim - = 1,1 = 1 X -> Körülbelül X X Q X Bár a szövege tulajdonságok 3 kifejezés csak a két funkciót, de ugyanez a tulajdonság is fel lehet használni, ha egy nagyobb számos tényező. n és m 1 * G4 (sin * -f cos * x) sin x! 0 6. példa Ide lim ---- L-. Ez a kifejezés L x J feszültség lehet reprezentálni a termék a két tényező: [4 (SIN1 x + cos * *)] és alkalmazása az ingatlan 3, akkor ugyanezt a tulajdonságot az első tényező, megkapjuk lim [4 (sin * JC + cos2 x )] lim = XQX 0 4 * = lim lim (sin * x + COS1 X) lim = 4 • N = 4. X - * * húzási Property 4. hányadosa két egyenlő, a hányados az osztalék az osztó limit limit, feltéve, hogy a határ az osztó nem nulla. x -4-2 7. példa találunk lim -. X 1 * t Mivel lim (x + 2) = 4, lim (x - 1) = 1, akkor az ingatlan 4 X X X Z 1 * 2 + A 4 lim -
= - = 4. X-t * -1 1, ha az osztó nulla határértéket, akkor a határérték is privát, hogy tetszőleges számú függően az osztalék. Íme néhány példa. 8. példa Tekintsük ChAT lim -, ahol m egy egész szám X X> 0. Ebben a példában elválasztó határ nulla, mivel lim JCE = lim x-lim x »limx = 0. XX - * • 0 X O X Nézzük a lehetséges speciális esetekben. Ha a / = 1, akkor lim lim = egy lim - • lim - = oo in «Y * x. X X X 0 X * 0 A> 0 X 0 * L (cm kb .. 5, § 1, és a magyarázat védjegy oo egyenes. 2. § 3). Ha m = 3, akkor lim - = lim a- is. x „az R s Ha m = 5, akkor lim - = lim ZH1 = a lim x = 0 X O * X -► 0 x Megjegyzés, hogy a meghatározás a határ a hányadosa két funkció abban az esetben, amikor a korlátokat és az osztó, és az osztalék egyidejűleg nulla, egy olyan feladat, leggyakoribb és elméletileg az egyik legfontosabb. De ebben az esetben, a tulajdon 4 nem hasznos. Az ingatlan 5 (fontos korlát tulajdonság). Ha az M pont mozog önkényesen az x tengely mentén, közeledik a P pont, mint a határérték és a P pont nem esik egybe a származási, a csak két esetben: 1) ha F pozitív abszcissza, az M pont némi időt is pozitív abszcissza; 2) ha P negatív abszcissza és az M pont a bizonyos idő negatív abszcissza. Így: Ha a határ nem nulla, akkor bizonyos határidőn belül és a pre-limit, az értéke ugyanaz. 5. § A lim (1 + • *) *. Az e szám X 1 Tekintsük az (L + x) *. Ha x nullához, akkor a tartalmát a zárójelben közelít egységét. Ha x nem egyenlő nullával, a konzol nem lesz egyenlő az egyik; Ebben az esetben, ha x nagyobb, mint nulla, akkor a konzol egynél nagyobb, ha x kisebb, mint nulla, akkor a konzol egységnél kisebb. Tekintsük 1 lim (1 + x) x. Nem világos, hogy mit fog egyezni nyatsya, hiszen egy egynél nagyobb szám, épül a pozitív fokozat, és l száma kevesebb, mint egy, épül a negatív erő. Azonban nem lehet bizonyítani, hogy ez a határérték létezik. Ezt bizonyítja a részletes tanfolyamok. Számos egyenlő ezt a határt, betűvel jelöljük e. Ily módon, az e szám hívják lim (1 + x) *. X e szám egy irracionális szám, annak hozzávetőleges értéke (a belül egy ezred) 2,718. Úgy találtuk, a matematika, ahányszor száma I. Ez bebizonyította, hogy nagyon kényelmes, hogy a szám, az alap logaritmusának. Logaritmusok az alap e nevezzük természetes logaritmusa. Ezek kijelölt egy jel. Ezek a logaritmus túlnyomórészt elméleti kérdéseket. 1. példa Find jelző - • = x, van, hogy n - »- oo x -> - 0. Ezért, a (X * 4- 1 -). Ehhez az átalakításhoz. * / Zable lim = lim ^ 1. jelölő = Bu dem van: lim (. \ - \ - \ Y = lim (1 + a) * a = e x V oo), és körülbelül REMARK. Mivel e értéke> 1, akkor lim ex = ∞, a lim ex = CO X O X (lásd. A vége § 3).