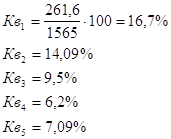A számítás a statisztikai mutatók
A munka leírása:
Munka típusa: kézikönyv
Képződése információs bázis - a kezdeti szakaszban a gazdasági és statisztikai kutatás. Számítások átlagos és marginális mintavételi hiba. Grade Distribution minta adatait a lakosság körében. Építése a növekvő számú változat.
Szabad számítás statisztikai mutatók
Letöltés A statisztikai mutatók
A szöveg a munka:
A magatartás statisztikai megfigyelési kialakított információs bázist. Létrehozása egy ilyen adatbázis - a kezdeti szakaszban a gazdasági és statisztikai kutatás. Az eredmények szerint a statisztikai megfigyelési kialakított információs adatbázis.
Annak megállapítására, a mintavételes felmérés program szükséges meghatározni a minimális mintanagyság, amely biztosítja a szükséges pontosságot. Számítási módszer minta n szám függ a választott módszer, ez képlettel számítjuk ki a táblázatban megadott. 1.
A számítás a minimális mintanagyság
Formula térfogatú mintát
Például, a fémfeldolgozó üzlet 100 hegesztők. Mert ez a gyűjtemény a szükséges mintanagyság. A rendszer segítségével a mintavételi módszer csere nélkül azt vártuk, hogy a mintavételes felmérés, hogy meghatározzuk az átlagos fizetés a workshopok hegesztők. Határozza meg a szükséges mintanagyság lesz ellátva valószínűsége 0,954, hogy a mintavételi hiba nem haladja meg a 190 p. a standard deviáció 490 p.
Helyettesítse a feltételezett érték (1), megkapjuk a minta minimális mennyiség:
A minta minimális mérete 22 egység.
Ki a bolt véletlenszerű mintavétellel csere nélkül mintavételi rabochih- kiválasztott 22 hegesztők, akik készülnek formájában információs adatbázis, a 2. táblázat mutatja.
ahol - a mintavételi hiba az átlag;
- A minták száma egységek;
- Az egységek számát a lakosság körében.
A számítás a teljes mintán átlagosan képletű:
Teljes fizetés helyettesíti a teljes minta a 2. táblázatban a (3) képlet és a tagok számát minta kapjunk
Gyártunk közbenső számítások és megjeleníti az eredményeket a 3. táblázatban.
A példánkban a marginális hibát képlettel számítottuk ki
Kiszámítása után a határ mintavételi hiba a megbízhatósági intervallum Bohl. Mert megbízhatósági intervallum adja meg:
Megosztani a megbízhatósági intervallum által meghatározott képlet szerint:
Behelyettesítve a számítás eredménye, amelyet a képlet (4) a (2) képlettel és (5), megkapjuk az átlagos hiba és a határérték eltérése:
Behelyettesítve a számítási eredmények a (7) képletű, megkapjuk a korlátokat a megbízhatósági intervallum:
4.Otsenka terjedési minta adatokat általános
Ha átlagbér munkás 2474,6 p. és a maximális mintavételi hiba 214,8, akkor ismerve a dolgozók száma üzlet = 100, be lehet állítani, hogy elfogadott határértékeket valószínűség alap bérüket.
5. Építőipari rendezett sorozat
Variációs sorozat - a sorozat által konstruált változókat. Ebben a tanulmányban az építési történik egyre több változatban. (Lásd. 5. táblázat).
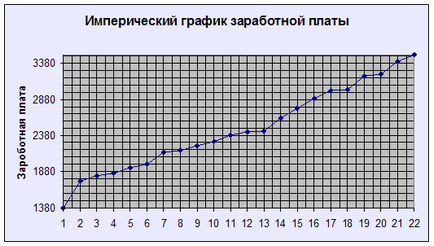
6. Építési ütemezni empirikus
Menetrend szerint épült a növekvő számú változat. A vízszintes tengelyen a számát mutatja a sorrendben egy több változatban. Az ordináta hatékony jele, ebben a példában, a bérek fizetett munkások. (Lásd. 1. ábra)
7. Szövegezési csoportok és kiszámítása indexek csoportok
Az első lépéseként a csoportok a számítás a csoportok száma és mérete az intervallum, amelyre az egyesített minta van törve.
Ahhoz, hogy megtalálja a csoportok száma egy Sturges képlet:
ahol n - a csoportok száma,
N - egységek száma a minta.
Ezt meg lehet határozni intervallum érték egyenlő időközönként az alábbiak szerint:
ahol - a legnagyobb index értéke,
- a minimum érték az index,
Határ értékei minden egyes csoport meghatározása a következő:
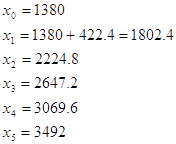
Így, az eredeti adatok vannak osztva az alábbi 5 csoportba:
Minden csoportban az átlagos szám értékét. Ez a számítás szerint végezzük a képlet:
ahol - az egyes értékek a csoport, például a fenti;
n - az egységek száma a csoportban, például, az első.
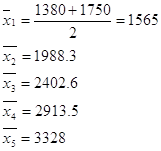
a csoport index kiszámítása az alábbi képlet segítségével:
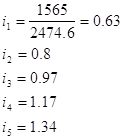
A számított adatok kerüljenek be a táblázatban. 6. és terjesztésére vonatkozó adatok több változatban a nevében.
ahol - az egyes jellemző értéket csoport izo-
- az átlagos értéke a jellemző csoport i-
k - az egységek száma a csoportban jelek
Behelyettesítve adatai 7. táblázat a (17) képletű, számítsuk ki a csoportközi variancia:
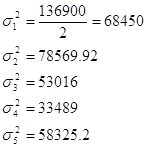
Kiszámítjuk az átlagos belüli variancia:
Két-csoport variancia kiszámítása:
A teljes variancia lesz egyenlő:
Elemi transzformációk általános képletű (16) eredményez képlet a diszperzió a momentumok módszerével:
Kiszámítjuk szórása csoportok és aggregátum:
A teljes standard deviáció szerint határozzuk meg ezt a képletet:
A korrelációs együttható alábbi képlettel számítottuk ki:
A meghatározás együtthatója alábbi képlettel számítottuk ki:
Együttható oszcilláció vagy relatív nagysága Kn.
ahol - az átlagos csoport vagy lakosság.
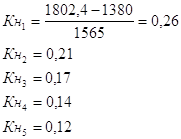
A variációs koefficiens formula határozza meg: