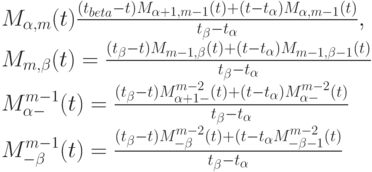Tudd Intuíció, előadás, görbék és felületek számítógépes geometria, ii

Let - egész. Tekintsük az egy fix funkció tekinthető funkciót hívjuk csonka exponenciális függvény.

Lemma 6.1. A származékok csonka exponenciális függvénye a következő képlet

Jelölje osztott különbség érdekében funkciókat építettek át a helyszínek rögzíteni csúcshalmazra és megvizsgálja a funkciót, ahol a megosztott különbség kiszámítása szempont függvényében rögzített

Lemma 6.2. Akkor hadd esliili

Megjegyzés 6.1.1. Lemmából 6.2 következik, hogy ha egy folytonos paraméter függvényében eltér a nullától csak

Példa 6.1.2. Osztott ötödrendű különbség csonkított harmadfokú egyenlet. Osztva a kiszámított különbség tekinthető funkció egy meghatározott program szerint az eltűnő a megosztott különbség egyáltalán fekvő balra és jobbra összes csomópont.

Alapján az osztott különbségek fogjuk építeni a súlyozó függvény az (6.2) abból a célból, általánosítás racionális Bezier görbéket:

Definíció 6.1.2. Normalizált B-spline m-edik érdekében nem csökkenő sorrendje csomópontok számít az első csomópont egy funkció

Ennek megfelelően, a nem normalizált B-spline egy olyan funkció,

Definíció 6.1.3. Normalizált B-spline m-ed rendű egy nem csökkenő sorrendje csomópontok számítva az utolsó csomópont egy funkció

Ennek megfelelően határoztuk meg a szabálytalan és a B-spline:

Megjegyzés 6.1.2. Ha a sorrendben a B spline meghatározására nem a csomópontok száma mínusz egy, és a mértéke csonkított funkció (például polinom t), majd a fent bevezetett -splines B lesz (definíció szerint) sorrend m. és (m - 1). Ebben az esetben más elnevezések vonatkoznak rájuk: Így

Mindkét megnevezések vannak jelen a szakirodalomban a B-görbét. Fogjuk használni az első. A Mathematica használt második.

Úgy véljük, (az egyszerűség kedvéért) mindkét irányban végtelen sorozata nem csökkenő minden csomópontot, ahol a fix meghatározott beállított B Ezután -Splines: spline csatolt egy csomóponthoz, mint egy első csomópont, spline csatolt egy csomóponthoz, mint utolsó csomópont

Lemma 6.3. Ha ez közül a funkciók és szolgáltatások csak m-rel a két osztály lehet eltér a nullától pont eltér a nullától a pont csak a következők lehetnek:

Lemma 6.4. Mert bárki, akinek van egy hely

6.2 Tétel (Cox képletű - de Boer). A következő képlet a nem normalizált B-spline bármely és: