Koordinátor módszer - studopediya
Probléma 1. A hossza Egy derékszögű háromszög egyenlő a és b. A átfogója a négyzet, a háromszög épül. Bizonyítsuk be, hogy a távolság a csúcsa a derékszöget zár be a tér közepén egyenlő.
Bemutatunk egy koordináta rendszerben. Mi választjuk ki a derékszögű csúcs, mint egy eredetű, és egy tengely mentén irányul a másik két oldal egy háromszög (ábra. 14).
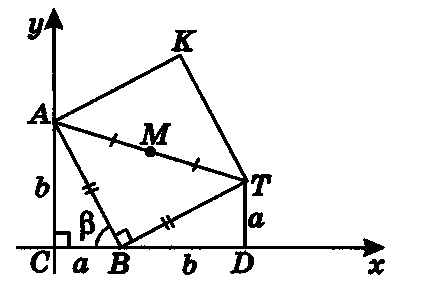
AKTV a tér közepén - a közepén a átlósan. Egy pont a koordinátái (0; b). Ahhoz, hogy megtalálja a koordinátákat a T pont, tartsa TD ⊥ Cx derékszögű háromszög, és hasonlítsa össze a BDT és az ICA. Ezek mentén átfogója, és hegyesszöget (AB = BT, mint az oldalán a tér, egy ∠TBD = 180 ° - - 90 ° 90 ° = - = # 8710; BAC). Ezután BD = AC = b, TD = BC = a. Ennélfogva, a pont koordinátái T lesz T (a + b, a). M - a középpontját a AT, így
=;
=.
A származási C koordinátái (0, 0), majd CM = =.
Probléma 2. igazolja, hogy az egyik a belső háromszög szögeinek ABC tompa, ha A (3; 5; 3) és B (2; 1, 4) és a P (0, -2, 1).
Találunk hosszát a háromszög oldalai a képlet két pont közötti távolság: d =.
Tekintsük a számának arányát kifejező négyzetének oldalán a háromszög: 38 + 14 = 52, 62> 52, azaz, ...
Következésképpen, az AC oldalon szemben a tompaszög B.