Az ingatlan egy lineáris egyenletrendszer triviális egyenlet
Szabály a mátrix szorzás
Tegyük fel, hogy 2-es mátrix A (m × n) és a B (n × l), és az oszlopok száma a mátrix A jelentése a sorok számát a mátrix B. Ezután a C mátrix (m × l) az elemekkel. (Azaz i-edik sorának az A mátrixot, szorozva egy skalár on j-edik oszlopa B mátrix, ad dik eleme CIJ a C mátrix, állva az i-edik sorának és j-edik oszlop).
. .
Az ingatlan egy lineáris egyenletrendszer triviális egyenlet.
Triviális egyenlet - az egyenlet, amelyben együtthatóinak az ismeretlenek és ingyenes szempontjából nulla.
Tétel: Egy lineáris egyenletrendszer tartalmazó triviális egyenlet egyenértékű a ugyanazt a rendszert anélkül, hogy a triviális egyenletet.
Bizonyítás: Tekintsük az esetben (1), és az azonos SLE (2), de nem triviális egyenlet.
Hagyja, hogy a vektor a megoldást a rendszer (1), mivel ez a vektor a megoldást a (2).
Megfordítva, tegyük fel, hogy a vektor a megoldást a rendszer (2). mert n-dimenziós vektor, és L a triviális egyenlet megoldása, ez a megoldás (1).
Így a lineáris egyenletrendszer tartalmazó triviális egyenlet egyenértékű a ugyanazt a rendszert anélkül, hogy triviális egyenlet.
Az ingatlan áll rendelkezésre az engedélyezett ismeretlen SLU
SLU úgynevezett megengedett. ha minden egyenlet a rendszer tartalmaz legalább egy engedélyezett ismeretlen.
Tétel: Ha engedélyezett SLE (4), így a szabad ismeretlen tetszőleges értékeket. t. e .. létezik egy egyedülálló megoldás a rendszer formájában egy n-dimenziós vektort K, amely koordináta értékek megfelelő szabad ismeretlen, rendre egyenlő.
Behelyettesítve a (4). Ezután hagyjuk ismeretlen értékek olyan lesz, hogy:
T. k. Vektor felhívja minden egyenletét a rendszer (4) a pontos numerikus egyenlőség, ez a megoldás ennek a rendszernek. Így, bebizonyítottuk a létezését megoldások a rendszer (4).
Annak bizonyítására, egyediségét egy ilyen megoldás. Hagyja, hogy a vektort ugyanazzal értékek ismeretlenek kapható oldat (4). Ezután helyettesítse be (4), kapjuk:
Ötvözi (5) és (6), azt látjuk, hogy. Így, ha bebizonyosodik, hogy létezik egy egyedülálló megoldás a (4) előre meghatározott értékekkel elérhető ismeretlen.
1) Mivel a. Szabad ismeretlen értékeket lehet beállítani végtelen sok módja van, a rendszer (4) bizonytalan.
2) Felbontás SLU mindig kompatibilisek. Ebben az esetben meg van határozva. ha m = n. t. e. száma egyenletek száma megegyezik az ismeretlenek, és nem határozza meg. ha a szám a egyenletek kisebb, mint az ismeretlenek száma, t. e. m Megoldás a rendszer homogén egyenlet Lineáris egyenletet homogénnek nevezzük. ha a konstans tag nulla, és különben inhomogén. Egy rendszer, amely a homogén egyenletek homogénnek nevezzük, és az általános formája: 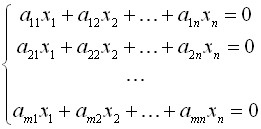
Tétel. Homogén lineáris egyenletrendszer egy triviális megoldás akkor, ha a rang kisebb, mint az ismeretlenek száma.
Bizonyítás: Tegyük fel, hogy a rendszer, melynek rangja egyenlő. Ez egy nulla megoldás. Nyilvánvaló, hogy nem haladja meg. Amennyiben a rendszer egy egyedülálló megoldás. Mivel a rendszer homogén lineáris egyenlet mindig a triviális megoldás, ez egy nulla megoldás, és ez az egyetlen megoldás. Így a nem nulla megoldások csak akkor lehetséges, ha.
Következmény 1: A homogén egyenletrendszert, amelyben száma egyenletek kevesebb, mint az ismeretlenek száma mindig nem nulla megoldás.
Bizonyítás: Ha az egyenletrendszert. A rangsorban a rendszer kevesebb, mint ahány egyenlet. azaz . Így az a feltétel, és ezért, a rendszer egy nem nulla oldatot.
Corollárium 2: A homogén rendszer egyenletek ismeretlenek van egy nem-triviális megoldás, ha, és csak akkor, ha determinánsa nulla.
Bizonyítás: Tegyük fel, hogy egy lineáris homogén egyenletek létrehozása, melyek mátrix determinánsát. Ez egy nulla megoldás. Ezután a tétel. ami azt jelenti, hogy a mátrix degenerált, azaz, .
Példák lineárisan függő és lineárisan független vektor rendszerek
1) A rendszer m-dimenziós vektorok úgynevezett lineárisan függ. Ha a lineáris egyenletrendszer (1) nem nulla megoldásokat. Ha a rendszer (1) nincs nem nulla megoldások, ez a rendszer a vektorok lineárisan független.
2) m-dimenziós vektorok úgynevezett lineárisan függő rendszerben. ha van egy nem nulla vektor. hogy tartja lineáris kapcsolat (2). Ha az arány a bármilyen típusú (2), hogy a. A rendszer a vektorok úgynevezett lineárisan függetlenek.
Példák lineáris programozási feladatok: kimenet, diéta, közlekedés, értékpapír-portfolió.