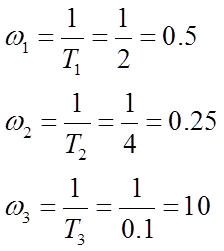Vizsgálata stabilitásának lineáris automatikus ellenőrző rendszerek
Stabilitásának vizsgálatára az ACS módszer Hurwitz
1) átviteli függvénye az ACS a zárt helyzetben:
A megfogalmazás kriteriyaGurvitsa:
A stabilitása ACS szükséges és elégséges, hogy az összes diagonális kiskorúak a Hurwitz determinánsok pozitív volt.
2) Find a karakterisztikus egyenlet adott rendszer
Nullának nevezője az átviteli függvény:
Jelöljük az együtthatók az egyenlet, és megtalálja a jelentésük:
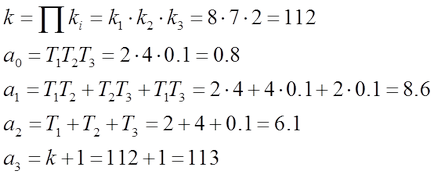
A karakterisztikus egyenlete a zárt lesz:
3) Írunk meghatározója Hurwitz:
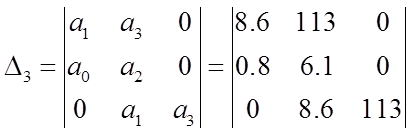
mert Aztán arra a következtetésre jutunk, hogy egy adott rendszer instabil.
4) hatásának meghatározását rendszer paramétereinek a stabilitását.
Kiszámítjuk a határértékek és a rendszer paraméterei:
Erre a célra, írunk az előre meghatározott feltétel megállapítása SAU stabilitását határ
Fejezzük ki a kívánt értéket:
Vegyünk egy ismeretlen paraméter, és írjon a stabilitási feltétel határ:
Mi eltávolítja a zárójelben, és oldja meg a kapott másodfokú egyenlet
(Régebben a laboratóriumi munka)
Annak megállapításához, a hatása ennek a paraméternek a stabilitást adott ACS tovább kell vizsgálni a rendszer stabilitását csökkenő és növekvő paraméter tekintetében a határait.
Stabilitásának vizsgálatára az ACS Nyquist kritérium
Formálási Nyquist stabilitási kritérium: ha a nyílt hurkú rendszer stabil, akkor a stabilitását egy zárt rendszer szükséges és elégséges, hogy APFC nyitott hurokban ω változik nullától ∞, nincs bevonva a pont koordinátái (-1; i0).
APFC nyílt hurkú rendszer a következő:
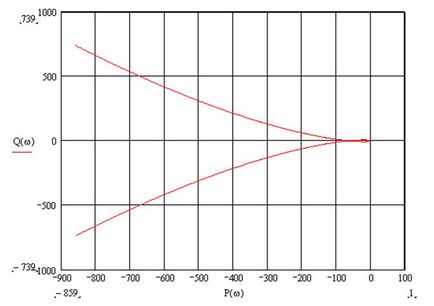
Attól függően, hogy milyen lehet mondani. Ez a nyílt hurkú rendszer instabil, és ezért lezárta is.
3. Kísérleti eredmények hitelességének.
3.1) Egy adott ACS távolítsa el a menetrend átviteli függvény és a fejében, hogy meghatározzuk a rendszer stabilitását.
A blokk-diagramja az adott paraméterek (a MATCAD program):
ACS előre meghatározott tranziens válasz:
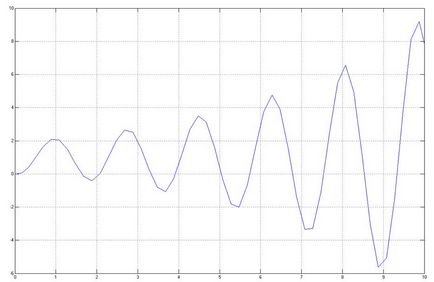
3-2) vizsgálata befolyása az együttható a rendszer stabilitását: határozzuk meg (empirikusan), a határ érték az átviteli együttható, és segítenek megtalálni a régió stabilitását (instabilitás). Vegyük ki a grafikus átviteli függvények stabil és instabil üzemmódok és a stabilitás a határ.
Módosítsa az értéket az egyik egyedi együtthatók Legyen, akkor lépés válasz lesz a következő formában:
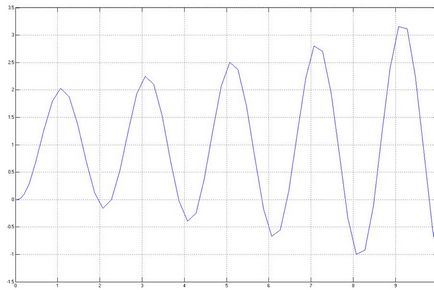
Tegyük fel, és a tranziens válasz lesz az alábbiak szerint:
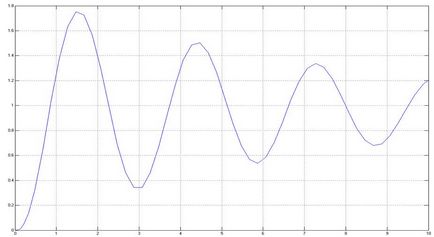
Felvette ugyanúgy, azt találjuk, hogy egyenlő 1,15, a határ a zárt rendszer átviteli együttható:
Amikor az átviteli sebesség egy zárt rendszerben, mint átviteli karakterisztikáját az a forma:
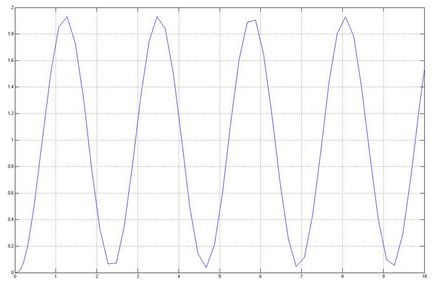
Arra a következtetésre jutottunk, hogy az ACS van a határ a stabilitás és a stabilitást a régióban.
3.3) Állítsa modell alapjel átviteli és hatásának vizsgálatára az időállandó együttható a rendszer stabilitását: meghatározza a határ értékeket az idő állandó, és segítenek megtalálni a régió stabilitását (instabilitás). Vegyük ki a grafikus átviteli függvények stabil és instabil üzemmódok és a fenntarthatóság határait.
Egy adott értéket időállandója tranziens formában van:
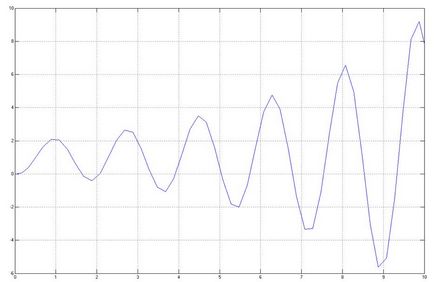
A változó értékét egy nagy és egy kisebb kéz, és távolítsa el a tranziens jellemzői:
Let értéke 0,15, akkor
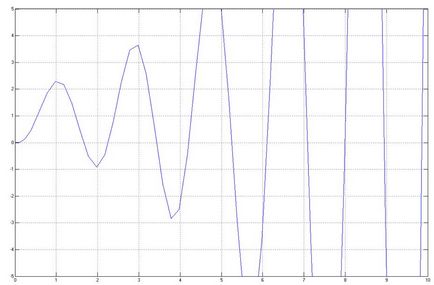
Hagyja, hogy a értéke 0,055, akkor
A rendszer stabilitására határ, tehát egyenlő 0,057
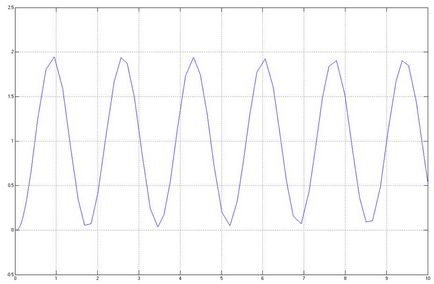
Ha megteszi a T értéke kisebb, a tranziens válasz, hogy stabil, ami azt jelenti, hogy a stabilitási tartomány. Legyen T = 0,03.
Ütemezése tranziens válasz ebben az esetben a következő lesz:
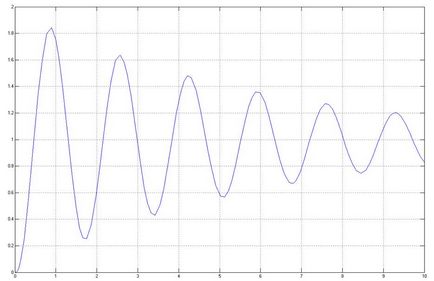
Tranziens válasz stabil, akkor a stabilitás domént helyesek.
Meg kell jegyezni, hogy van egy másik terület stabilitását kapott elméletileg meg lehet írni, mint :.
3.4) Vegye ki a frekvencia karakterisztika A (ω) és φ (ω) egy adott ACS és a nyitott helyzetben rajta, hogy ellenőrizze a rendszer stabilitását Nyquist kritérium. Ha kiveszi a frekvencia karakterisztika a frekvencia kell hoznia kapcsolási egység.
Tedd az jesítményszint bemeneti jel harmonikus, a blokk diagram válik:
Változtatásával a forrás frekvencia ω eltávolítani a függőség A (ω) és φ (ω), az adatok a táblázatban szereplő:
Frekvencia interfész egységek szerepelnek előre meghatározott azonos SAU