normális eloszlás

Home | Rólunk | visszacsatolás
A meghatározás szerint a sűrűsége normális eloszlású véletlen változó értéke
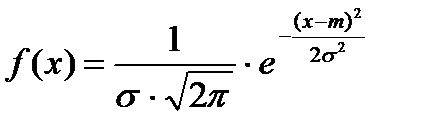
Lehetséges értékeit az X változó vehet minden valós értékek -∞<Х<∞, а распределение зависит от двух параметров. -∞ Így, a grafikon a f (x) jelentése: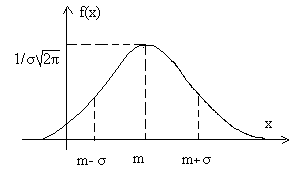
Ha m = 0, és # 963; = 1. a törvény a normális eloszlás az úgynevezett szabvány. Ebben az esetben,
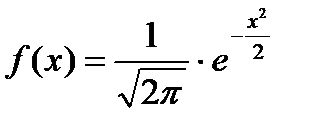
Ha az X valószínűségi változó oszlik szerint normális eloszlású paraméterek m és # 963;. ezt a tényt kell rögzíteni, így.
Kiszámoljuk a várakozás egy véletlen változó
Így a paraméter m - a matematikai elvárás egy véletlen változó X.
Most kiszámítani a variancia
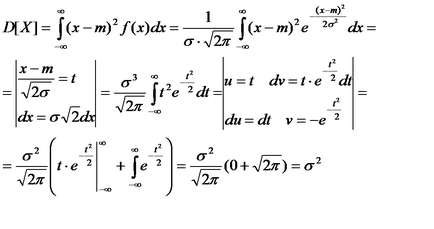
ahol már használják azt a tényt, hogy a szabály L'Hospital
Így a paraméter # 963; - a standard deviáció, mert # 963; 2 - a variancia.
Mode és a medián normális eloszlás egybeesik azzal az elvárással, mert max f (x) érjük az x = m és
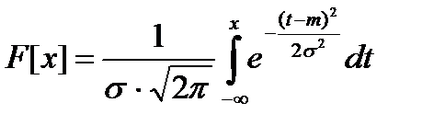
eloszlásfüggvénye a törvény, amely a grafikonon látható az ábrán.
Nézzük számítani P (a<Х ahol alkalmaztuk a Newton-Leibniz formula határozott integrálok, és - bármely antiderivált a integrandust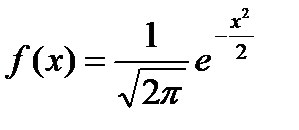
Bármilyen primitív lehet kiszámítani a következő képlettel
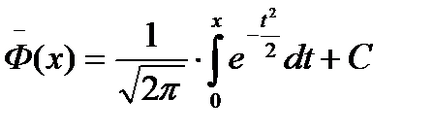
ahol C - egy tetszőleges konstans. Ezt könnyen ellenőrizheti az Diffie-levezetést.
Amikor C = 0, megkapjuk a Laplace funkció
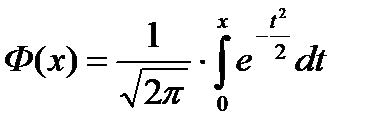
és amikor a C = ∞ - standard normális eloszlásfüggvény
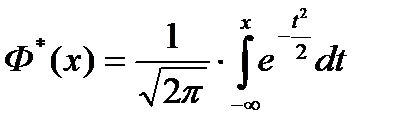
Attól függően, hogy a rendelkezésünkre álló keze alatt a táblák, fogjuk használni egy adott képlet. Megjegyezzük, hogy a használata a táblákat a Laplace funkció hasznos, mert ez nem igaz, és mi könnyen - talál érték negatív érv (általában szereplő táblázat csak a pozitív értékek az érvelés). Felhasználás táblák f (x) ebben az esetben kissé kényelmetlen, ha azt kizárólag a pozitív értékek az érvelés.
1. példa Tegyük Nézzük mi annak a valószínűsége, hogy X értékét veszi intervallumban] 0 3 [.
A táblázat szerint a Laplace funkció kap
A táblázat szerint az eloszlási függvény a standard normális törvény úgy kapjuk meg kapcsolatát a Laplace funkció:
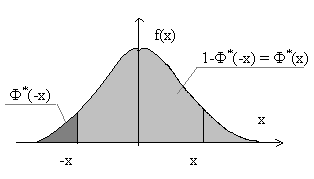
amely könnyen menet a biztonsági öv a következő ábrán.
Mi található a valószínűsége, hogy a hit a normál eloszlású véletlen változó intervallum] m-l, m + l [, szimmetrikus az átlag:
Ha l kap a különböző
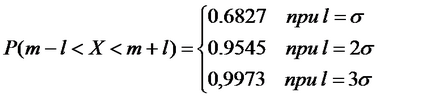
Amint láttuk, bár ez elméletileg lehetséges értékei az X lehet bármilyen, de gyakorlatilag az összes érték tartományba esnek] m-3 # 963 ;, m + 3 # 963; [. Ezt a tényt a szokás nevezni a szabály „három szigma”. Egy normális eloszlás 10.000 mérés, csak 27 van egy „legális” joga van elállni az intervallumban (valószínűtlen, és ez általában elhanyagolt). Ezért feltételezhetjük, hogy minden lehetséges értéket cart-normál eloszlású véletlen változó ebbe a tartományba esik.