Sűrűség az aránya a testsúly a térfogatához
A SI rendszerben, a sűrűséget kg /. és a CGS rendszer gramm /.
Fajsúly az aránya a testsúly a térfogatához
A fajsúly mérjük SI H / m 3, és a CGS rendszer din / cm 3.
Newton szerint második törvénye tömege P = mg, ahol a g - a nehézségi gyorsulás. Ezután az aránya is képviselteti magát a terméket a test sűrűsége a nehézségi gyorsulás:
Amikor a változás a testhőmérséklet és megváltoztatja annak sűrűsége, ahogy változtatja meg a térfogatát. A függőség a sűrűsége a testhőmérséklet képlete:
ahol - sűrűsége 0 ° C-on - együtthatója térfogati expanziója a test, T - a testhőmérséklet.
Számos módja van meghatározására sűrűségű szilárd anyagok. Ha a test egy szabályos mértani forma, annak sűrűségét könnyen mérésével határozzuk meg a térfogatához és tömegéhez. Ha a test szabálytalan geometriai alakja, a térfogatát meghatározzuk a főzőpohárba eljárás vagy alkalmazás, hidrosztatikus súlyú. Annak megállapításához, a bírság és a szemcsés szilárd anyagok, valamint, hogy meghatározzák a sűrűsége a folyékony használt speciális eszköz - piknométer.
Ebben a laboratóriumi munka határozza meg a sűrűsége a szilárd anyagok szabályos mértani forma, melynek térfogata a könnyen kiszámítható a megfelelő képlet alkalmazásával.
Szervei által szabályos mértani forma, így különösen: a labda, amelyre a következő összeget:
ahol R - sugara, D - átmérője a labda.
A henger, amelyek összege:
; ahol D - a henger átmérője H - magassága.
Egy üreges henger, amelynek a térfogata;
ahol D - átmérője a külső henger, H - magassága, d - a belső átmérője a henger.
Paralelepipedon amelynek térfogata V = a * b * c. hol és - a magasság, b - hossz,
c - a szélessége a doboz.
II. ORDER TELJESÍTMÉNYÁLLANDÓSÁG
1. Határozza meg a tömeg egy test technikai szinten, a szabályok betartása mellett a velük dolgozni. Figyeljünk a pontosságát súlyú technikai egyensúlyt.
2. Mérjük meg a lineáris méretei a féknyereg test. Tedd mérés háromszor, majd számoljuk az átlag.
3. Az átlagértékeket lineáris méretek, kiszámítjuk a szervezetben.
4. Mérjük meg a lineáris test mikrométer nagyságrendű (háromszor mindegyik méret), és kiszámítja az átlagos adatok a test teljes térfogatában.
5. Kiszámítjuk az átlagos sűrűsége a test a tömegértékeket és a test térfogata
külön-külön a féknyereg testméretek és mikrométeres
6. Számítsuk abszolút testtömeg mérési hiba, és a lineáris méretei a szervezetben.
7. Számítsuk ki a relatív hiba a sűrűségmérés test képlet:
ahol m - az átlagos értéke a testsúly, - átlagos abszolút hiba mérésére testtömeg, - mérjük a térfogat szerinti átlagos relatív hiba (a képlet a relatív mennyisége a test a mérési hibák vannak megadva a megjegyzések ehhez papír).
8. Számítsuk abszolút sűrűsége mérési hiba a következő képlet segítségével (külön kaliper és mikrométeres):
9. Ezek a mérések és számítások, tárolja a táblázatban.
10. Rögzítse a választ a következő formában: Külön mérő féknyereg és mikrométeres sűrűsége a szervezetben.
11. értékelje a relatív hiba sűrűség mérés és adatgyűjtés százalékában a 2. táblázatban.
12. következtetéseket levonni.
Mennyiségének meghatározásakor a test
Képletek kiszámításához relatív térfogat mérési hibák szervek szabályos mértani forma
ahol D - átlagos átmérőjű értéket, # 916; D - átmérője az átlagos abszolút hiba a mérések.
ahol D és H médián átmérő és a magasság, illetve # 916; D és # 916; H - átlagos átmérője abszolút mérési hiba, és a henger magassága.
Egy üreges henger :,
ahol D és D - az átlagos értékek a külső és belső átmérők, illetve, # 916; D és # 916; d - az átlagos értékei az abszolút hiba a mérések a külső és belső átmérők, illetve H - átlagos magassága a henger, # 916; H - átlagos értéke a abszolút magasságát mérési hibák.
ahol a, b, c - az átlagos értéke a magasság, hosszúság és szélesség, illetve # 916; a, # 916; ben, # 916; s - átlagos abszolút mérési hibákat.
1. Milyen méréseket úgynevezett közvetlen és közvetett? Adjon példát.
2. Milyen hibákat nevezik szisztematikus és random? Ahonnan függ?
3. Melyek a mérési hibák nevezzük abszolút és relatív? Mi az a dimenzió ezeket a hibákat?
4. Adja meg a koncepciót a súly és a testtömeg, sűrűsége és fajlagos sűrűsége. Melyek a mértékegységek ezek az értékek?
5. Fogalmazza Newton és a gravitáció törvényét.
7. Hogyan működik a sűrűsége a hőmérséklet?
Laboratóriumi munka №2
Tanulmány a törvények a rezgőmozgás egy egyszerű inga és mennyiségi meghatározása a nehézségi gyorsulás.
Célkitűzés: A tanulmány a törvények a rezgőmozgás. meghatározzák a nehézségi gyorsulás.
Eszközök és kellékek: matematikai inga, stopper, meg a golyók, egy vonalzóval.
1. Rövid elméleti információkat.
A mozgalom, amelyben a szervezet vagy szervezetek a rendszer szabályos időközönként eltér az egyensúlyi helyzet, és visszatér oda, az úgynevezett időszakos rezgéseket.
Ingadozása, amely az idő múlásával változik a rezgő értékek a törvény szerint a szinusz vagy koszinusz, az úgynevezett harmonikus.
Harmonikus rezgés egyenlet felírható:
A harmonikus rezgéseket jellemzi a következő paramétereket: az A amplitúdó, T periódus, a frekvencia # 965;, fázis # 966;, körfrekvencia # 969;.
A - amplitúdó rezgések - ez a legnagyobb elmozdulást az egyensúlyi helyzet. Az amplitúdó egységekben mérjük a hosszúság (m, cm t. D.).
T - rezgési periódus - az időtartam, amely alatt zajlik egy teljes oszcilláció. Az időszak másodpercekben mérhető.
# 965; - A mintavételi frekvencia - a rezgések száma előforduló egységnyi idő alatt. Mértékegysége a Hertz.
# 966; - fázisában az oszcilláció. Fázis meghatározza a helyzetét a rezgő pont egy adott időben. Az SI rendszerben a fázis radiánban.
# 969; - körfrekvencia mérjük rad / s
Bármilyen oszciiiáiómozgásban zajlik hatása alatt változó erő. Abban az esetben, harmonikus mozgás ez az erő arányos az elmozdulás ellen irányul bias:
ahol K - együtthatója arányosság attól függ, hogy a testsúly és a körfrekvencia.
Egy példa a harmonikus rezgés lehet oszciiiáiómozgásban egy egyszerű inga.
Matematikai inga nevezzük anyagi pont felfüggesztve egy súlytalan és nem deformálható fonalak.
Kis nagy labda felfüggesztettek egy vékony szál (nem rugalmas), ez egy jó modell matematikai inga.
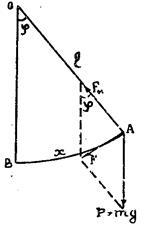
Legyen a matematikai inga L hossza (ábra. 1) el van térítve a egyensúlyi helyzet egy kis szög OB # 966; ≤. A labda gravitációs cselekmények. függőlegesen lefelé, és az erő rugalmassági izzószál. irányított menete mentén. A kapott F erő mentén irányul érintő a AB ív és egyenlő:
At kis szögek # 966; felírhatjuk:
ahol X - ív elmozdulása az inga az egyensúlyi helyzetből. Aztán kapunk:
A mínusz jel azt jelzi, hogy az F erő ellen irányul az elmozdulás X.
Így, az eltérés matematikai inga oszcillál kis szögek. Az az időszak, oszcilláció a matematikai inga által meghatározott Huygens:
ahol - .. inga hossza, azaz a távolság a pont a felfüggesztését az inga súlypontja.
Az utolsó egyenlet egyértelmű, hogy az időszak az oszcilláció a matematikai inga függ csak a hossza az inga és a gravitációs gyorsulás és független az amplitúdó-ingadozások és a tömeg az inga. Ismerve az időszak az oszcilláció a matematikai inga és annak hossza, lehetséges, hogy meghatározzák a nehézségi gyorsulás képlet szerint:
Nehézségi gyorsulás nevezik gyorsulás, hogy megkapja a test mellett a gravitációs erő a földre.
Ennek alapján Newton második törvénye és a gravitáció törvénye felírható:
ahol # 947; - a gravitációs állandó, egyenlő
M - a föld tömege egyenlő,
R - távolság a központtól a Föld egyenlő,
. Mivel a föld nem képez megfelelő labdát, majd különböző szélességi ez eltérő jelentéssel bír, és így a nehézségi gyorsulás különböző szélességi más lesz: az egyenlítő; a pole; A közepes földrajzi szélességeken.