Hesseni Matrix Online

előző ◈ a következő

Kétszer folytonosan differenciálható függvény f (x) egy konvex (konkáv) akkor és csak akkor, ha a hesseni f (x) x pozitív (negatív) szemidefinit minden x (lásd. A lényeg a helyi szélsőérték a sok változó függvénye).

A kritikus pont a függvény:

ha a Hesszeni pozitív definit, akkor x0 - egy helyi minimum pont a függvény f (x).
ha a Hesszeni negatív megadott, majd x0 - lokális maximum pontját az f (x).
ha a hesseni nem írja alá-biztos (megkapja a pozitív és negatív értékek), és a nem-degenerált (), majd x0 - a nyereg pont a függvény f (x).

Meghatározásának kritériumait mátrix (Sylvester tétel)

Pozitív meghatározottsága.

valamennyi átlós mátrix elemeinek pozitívnak kell lennie;
Több fő meghatározói pozitívnak kell lennie.

Pozitív szemidefinit mátrixok Sylvester kritérium hangzik: A forma pozitív szemidefinit, ha és csak akkor, ha a megbízó kiskorúak nem negatív. Ha a hesseni mátrix pozitív szemidefinit (összes fő kiskorúak nem negatív), akkor a minimum pont (ha azonban a hesseni szemidefinit, és az egyik kiskorúak 0, akkor ez lehet egy nyereg pontot. Szükségünk van további ellenőrzéseket). Pozitív félig határozott:

minden átlós elemek a nem-negatív;
az összes jelentős meghatározói nem negatív.

A fő meghatározója - a fő meghatározója a kisebb.

Tér szimmetrikus mátrix a rend n. amelynek elemeit másodrendű parciális deriváltjai az objektív függvény, az úgynevezett hesseni mátrix és jelöljük:

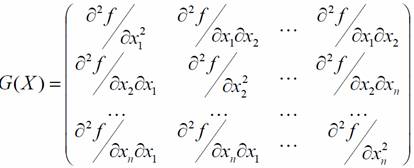
Szimmetrikus mátrix pozitív definit akkor, ha annak minden átlós kiskorúak pozitív volt, vagyis

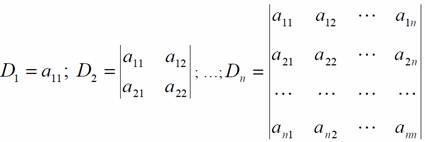
A mátrix A = (aij) pozitív.

Negatív határozott.
Ahhoz, hogy szimmetrikus mátrix negatívan meghatározva, szükséges és elégséges, hogy az egyenlőtlenségek:
(-1) k Dk> 0, k = 1. n.
Más szóval, annak érdekében, hogy a kvadratikus forma negatív határozott. szükséges és elégséges, hogy a jel a szögletes kiskorúak kvadratikus alak mátrix váltakoztak, kezdve egy mínusz jel. Például, a két változó, D1 <0, D2> 0.

Ha a hesseni szemidefinit, akkor lehet, hogy egy inflexiós pontja. Több kutatásra van szükség, ami lehet végezni az alábbi lehetőségek közül:

Csökkentése érdekében. Ez a változás a változók. Például, egy funkciója két változó az y = x. Ennek eredményeképpen kapunk egy funkciója egy x változó. Azt is vizsgálja, a viselkedését a funkciót a vonalak y = x és y = -x. Ha az első esetben a teszt funkció lesz egy minimális pontot, és egy másik esetben a maximális (vagy fordítva), a vizsgált pont egy nyereg pont.
Megtalálni a sajátértékei a hesseni. Ha minden érték pozitív, akkor a függvény a mérőpont van egy minimális, ha minden negatív - van a legnagyobb.
Study f (x) a szomszédságában ε. Az x helyébe x0 + ε. Ezután meg kell bizonyítani, hogy az f (x0 + ε) egyváltozós e, vagy nagyobb, mint nulla (a minimum pont x0), vagy kevesebb, mint nulla (ha a maximális pont x0).

Példa №1. Az alábbi funkciók domború vagy homorú: f (x) = 8x1 2 + 4x1 x2 + 5x2 2.
Határozat. 1. Keresse meg a parciális deriváltak.

2. Oldja meg az egyenletrendszert.
-4x1 + 4x2 +2 = 0
4x1 -6x2 +6 = 0
kapjuk:
a) Az első egyenlet Express x1 és a helyettesítő a második egyenletet:
x2 = x2 + 1/2
-2x2 +8 = 0
Tól x2 = 4
Ezek az értékek X2 behelyettesıtve x1. Kapjuk: x1 = 9/2
A számos kritikus pont egyenlő 1.
M1 (9/2; 4)
3. Tegyük a másodrendű parciális deriváltak.

4. kiszámítjuk az érték a másodrendű parciális származékok a kritikus pontok M (x0; y0).
Értékek meghatározásához azt a pontot az M1 (9/2; 4)

Épület egy hesseni mátrix:

D1 = a11 <0, D2 = 8> 0
Mivel az átlós kiskorúak különböző jelek, domború vagy homorú a funkciók nem mond semmit.

Példa №2. Határozza meg, hogy az f (x) = 2x1 + x2 2 2 + sin (x1 + x2) konvex a térben R2.
Határozat. Kétszer-differenciálható konvex függvény a térben R 2, ha a fő kiskorúak szögletes hesseni nemnegatív. Írunk a hesseni mátrix - mátrix második származékai:

Principal kiskorúak rendre:

Így, D1> 0, D2> 0 minden értékeket, azaz f (x) konvex.

Kapcsolódó cikkek

előző ◈ a következő