Darboux összegek
Jelöljük. .
Aztán az úgynevezett alsó és felső Darboux összegeket.
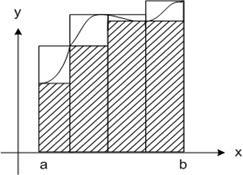
Ez a határ a teljes összeg Darboux a határ az integrál egyenlő összeg azonosítani határozott integrál.
= = =.
Geometriailag Darboux összegek négyzet lépésről, mint a számok megközelítő területe görbe vonalú trapéz által határolt grafikon és egyenes. Az alacsonyabb összeget - a megközelítés a fogyatékosság és a felső - bőségesen. Így a határozott integrál egy nem-negatív funkció a terület az íves trapéz.
Ahhoz, hogy integrálható függvény az intervallumon. folytonossága ebben a szegmensben nem szükséges. A elégséges feltétele az integrálhatóság az intervallum is szakaszonként folytonosság ebben a szegmensben.
A funkció felhívta egy szakaszonként folytonos intervallum, ha ebben az intervallumban véges számú pontot diszkontinuitás az első ilyen.
Példa. Számoljuk ki a területet az ábra által határolt parabola és egyenes.
Határozat. Elosztjuk az intervallum beilleszkedés egyenlő hosszúságú részre. - osztási pont. Figyelembe véve azt a tényt, hogy a funkció szigorúan növekvő intervallumon. Mi járna Darboux, és megtalálja a korlátokat, hogy mikor.
=. .
=.
.
Mivel - a területen sebesség számok, kisebb keresési terület, és
- területe lépés-szerű alak, a legtöbb a kívánt területre, a szükséges területet
=.
A határértékek az alsó és a felső Darboux összegek mérkőzés, így az intervallum funkció integrálható, és
.
Példa. A határozott integrál, hogy megtalálják a limit összeg
.
Határozat. Képviseli a szükséges összeget formájában szerves sum =. Ebben az összegben. de aztán
= (Per az előző példában).
Határozat. Hagyja, majd a jobb oldalon az azonosság
Ez könnyű észrevenni, hogy a bal oldalon a személyazonosságát is képviselteti ugyanabban a formában. Továbbra is azt mutatják, hogy van egy véges határa ez a kifejezés
a
=.
A kapott kifejezés a szerves Összegezve, ezért