lecke №54
· Oktatás - ismétlés, szintézise és tesztelése a tudás a témáról: „A helyek módszere” az alapkészségek.
· Oktatási - fejleszteni a tanulók figyelmét, szorgalom, kitartás, a logikus gondolkodás, a matematikai beszédet.
· Oktatási - keresztül bemutató nevelése figyelmes hozzáállás egymás felé, hogy átadják a képességgel, hogy hallgatni barátok, a kölcsönös segítségnyújtás, az önellátás.
I.Organizatsionny lépésben (2 perc)
II.Aktualizatsiya szubjektív tanulók (5 perc).
1) Mi az a kör?
2) Definiálja egy háromszög?
3) Mi a merőleges?
4) Mi az érintő?
5) Mi a felezővonal a háromszög?
III.Formirovanie képességek (20 perc)
A pontok helye (GMT) - ponthalmaz, amely bizonyos tulajdonság.
HMT ismert meg:
1. A merőleges a szegmens - a pontok halmaza egyenlő távolságra a végpontok.
2. Kerület - több pont egyenlő távolságra egy adott ponton - a kör közepén.
3. A felezővonal a szög - a pontok halmaza egyenlő távolságra oldalán a szög
· Így bizonyítjuk a tételt: a hosszára merőleges mértani-kim hely pont egyforma távolságra a végén ebben a szegmensben.
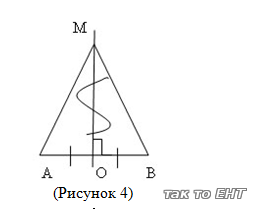
Adott: AB; Defense - a merőleges
Bizonyítsuk be: AM = BM
1. MO - a merőleges (a feltételezés) -> O - középső szegmenst AB. MO AB
2. Tekintsük a AMO és a WMO - négyszögletes
MO - közös láb
AO = VO (O - mid AB) -> AMO = WMO (2-m befogó) -> AM = BM (definíció szerint egyenlő háromszögek, a megfelelő oldalon)
QED
Házi feladat: „Ahhoz, hogy bizonyítani a tétel, az inverz e”
Tétel: „minden pontja egyenlő távolságra a végén a szegmens fekszik a merőleges ebben a szegmensben.”
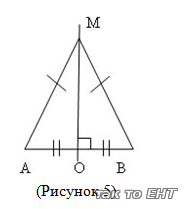
Bizonyítsuk be. M fekszik a függőleges felezővonal
1. Mivel MA = CF (a feltételezés) -> AMB - egyenlő szárú (definíció szerint).
2. Draw MO AB, azaz kihagyja hav.
3. Mivel AB - az alapja egy egyenlő szárú AMB, a Honvédelmi Minisztérium - a medián -> AO = OB (a Properties egy egyenlő szárú háromszög).
így Védelem - a merőleges, amely tartalmazza az összes pont egyenlő távolságra a végén a szegmens.
Az ingatlan midperpendiculars az oldalán a háromszög
Metszik egymást ugyanazon a ponton, és ez a pont a közepén a körülírt kör körül a háromszög, tanulmányozni fogjuk a nyolcadik évfolyam.
Célkitűzés: „A konstrukció a merőleges a szegmensben.”
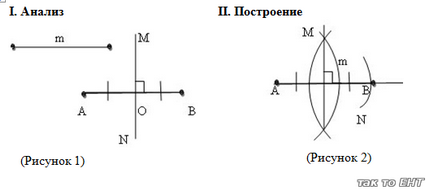
· Tétel. Felezővonal a pontok helye fekvő egy adott szög és egyenlő távolságra van az oldalán.
· Proof. Tekintsük csúcsszög C az O pont, és az oldalán egy, b. Hagyja, hogy a C pont fekszik egy adott szögben. Hagyjuk ki ebből a CA és CB merőlegeseket oldalai a és b (ábra. 2). Ha a CA = CB, a derékszögű háromszög AOS és VOS (mentén átfogója és egy láb). Következik-szekvenciát, a szögek AOC és BOC egyenlő. Ennélfogva, C felező pont tartozik. Ezzel szemben, ha a C pont tartozik a felezővonal a szög, a derékszögű háromszög AOC és BOC jelentése (a átfogója és hegyesszögben). Következésképpen, AC = BC. Ennélfogva, a C pont egyenlő távolságra levő oldalán a szög.
Feladat:
- Construct HMT távol az O pont egy r távolságtól.
- Építsünk lókusz egyenlő távolságra a végén a szegmens AB.
- Construct lókusz egyenlő távolságra az oldalán a szög.
- Építsünk HMT távoli vezetékes l egy h távolság.
1. Keresse locus központja a körök, amelyek átmennek a két adott pont.
2.Postroyte háromszög középpontja kör (egy kör áthaladó a csúcsai a háromszög).
V. házi (2 min.) №231,232,233 str74
VI .Podvedenie tanulsága eredményét (3 min.)
(A minőségi munkájának értékelése az egyes tanulók és osztályok).
VII .Etap reflexió (2 min.)